Clustering: HDBSCAN

딥러닝(neural network)이 비약적인 발전을 이룩한 이후 supervised 학습은 여러 측면에서 많이 발전 할 수 있었습니다. 하지만 unsupervised 학습은 아직 가야 할 길이 많이 남아있는 상황입니다. 오늘은 이 unsupervised 학습의 대표적인 문제인 clustering에 대해 다루고자 합니다. 크게 clustering 알고리듬은 아래 3가지 형태로 나뉠 수 있습니다.

Distance-based methods
Density-based and grid-based methods
Probabilistic and generative models

density-based 방법론 중 널리 알려진 DBSCAN (Density-Based Spatial Clustering of Applications with Noise) 방법을 개선한 아직은 널리 알려지지는 않은 HDBSCAN (Hierarchical DBSCAN)에 대하여 살펴보도록 하겠습니다.

DBSCAN remind

HDBSCAN 알고리듬을 설명 드리기에 앞서, 먼저 DBSCAN에 대해 잠깐 리마인드 하는 시간을 갖도록 하겠습니다.

DBSCAN에서 cluster의 정의는 density-connected point들을 최대로 포함하는 집합입니다. 그렇다면 density-connected point의 개념은 무엇일까요? 이를 이해하기 위해서는 먼저 아래 속성에 대한 이해가 필요합니다.

Eps(ε) : 클러스터에 이웃을 포함할 수 있는 최대 반지름 거리
MinPts : 클러스터를 형성하기 위해 필요한 최소 이웃 수

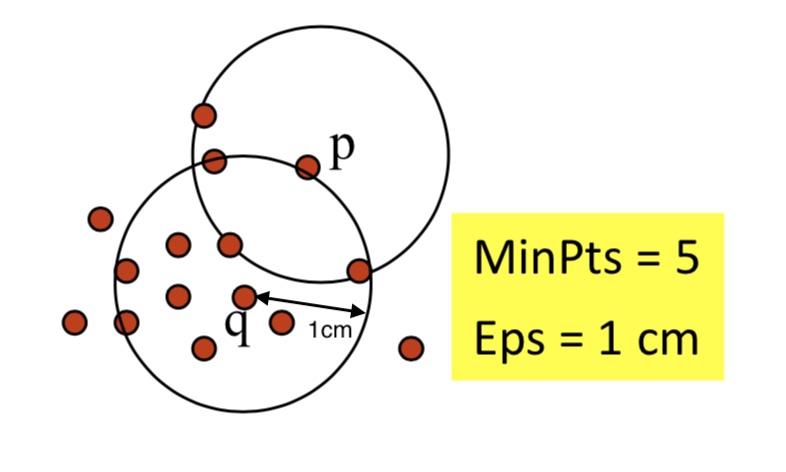
Eps, MinPts 개념

point q를 기준으로 클러스터 안에 포함된 number of points를 나타내는 함수를 정의해보면 다음과 같습니다.

\[NEps(q)= \left \{ p\ belongs\ to\ D | dist(p, q) ≤ Eps \right \}\]

그런 다음 위 개념을 토대로 directly density-reachable, density-reachable, density-connected에 대한 개념을 정의해 보면 아래와 같습니다.

Directly density-reachable

if ( p ∈ NEps(q) and |NEps(q)| ≥ MinPts ) then
point p는 q로부터 directly density-reachable 하다
end

Density-reachable

if ( there is a chain of points p1, ..., pn, p1 = q, pn = p such that pi+1 is directly density-reachable from pi ) then
point p는 q에 density-reachable 하다
end

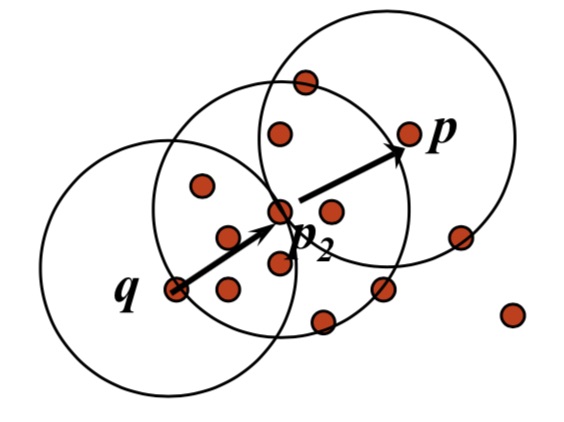
density-reachable 개념

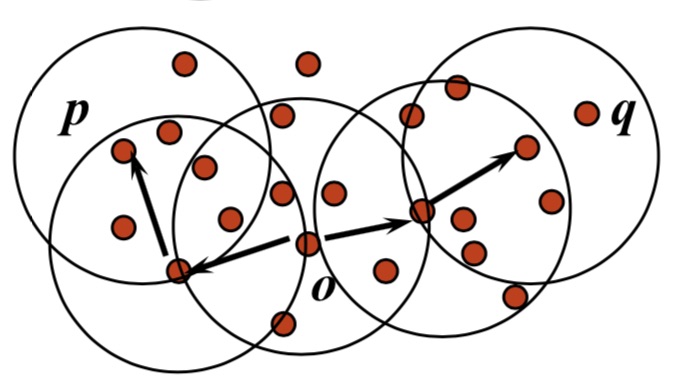
Density-connected

if ( there is a point o such that both p and q are density-reachable from o ) then
point p는 q에 density-connected 하다
end

density-connected 개념

마지막으로 DBSCAN 알고리듬 계산 과정을 정의하면 아래와 같습니다.

DBSCAN Algorithm
이미 선택되지 않은 point p를 임의로 고른다
p로부터 density-reachable한 모든 point들을 조사한다, w.r.t. Eps and MinPts
1. 만약 p가 core point (|NEps(p)| ≥ MinPts)라면, cluster를 만든다
2. 만약 p가 border point 라면, p에 density-reachable한 point가 존재하지 않기 때문에 DBSCAN은 1번 과정으로 되돌아간다
모든 point를 방문할 때까지 반복한다

* spatial-index를 사용하지 않은 일반적인 time-complexity는 O(n^2) 이다

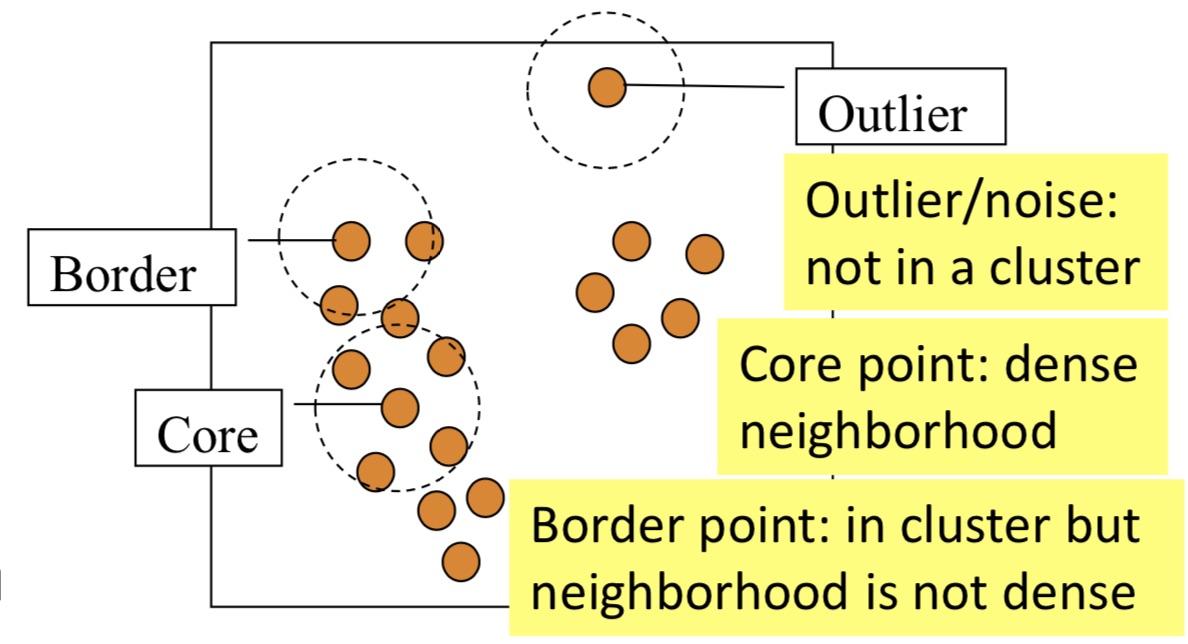
core, border, outlier 개념

알고리듬을 보시면 아시겠지만 DBSCAN의 결과는 모델의 hyper-parameter인 ε과 MinPts에 따라 상당히 다른 결과를 보여주게 됩니다. 아래 그림은 이와 같은 현상을 보여주고 있습니다.

hyper-param에 따른 결과변화

Figures from G. Karypis, E.-H. Han, and V. Kumar, COMPUTER, 32(8), 1999

하지만 대부분의 경우 우리는 적절한 ε과 MinPts 값을 알 수 없으며 이는 대부분 heuristic하게 학습 과정을 통해 결정하게 됩니다. 또한 dataset이 조금만 변하게 되더라도 이전에 결정된 ε과 MinPts값은 더 이상 최적의 값이 아닌 게 될 수 있습니다. 이런 부분들을 일부 개선한 것인 HDBSCAN입니다. 다음은 HDBSCAN에 대해 알아보도록 하겠습니다.

H-DBSCAN

HDBSCAN의 경우 ε 파라미터는 더 이상 필요하지 않으며 MinPts만 존재합니다. 따라서, hyper-parameter에 대한 tuning 비용이 상당히 줄어듭니다. 사실 MinPts 값은 대부분 학습 전에 직관적으로 정할 수 있습니다.

HDBSCAN 알고리듬 계산과정을 대략적으로 스케치해 보면 다음과 같습니다.

dataset의 값들을 density/sparsity 의미를 포함한 값으로 변환함
point간의 mutual reachability distance값을 기반으로 MST(minimum spanning tree)를 만듬
connected component들의 클러스터 hierarchy를 구축함
설정된 MinPts값을 기반으로 클러스터 hierarchy를 축약함
축약된 클러스터 hierarchy에서 stable한 클러스터만 선택함

각 단계별로 처리되는 로직에 대한 설명은 아래와 같습니다.

1. Transform the space

노이즈가 다수 존재하는 dataset 에서 적절한 클러스터를 찾기 위해서는 알고리즘을 실행하기 전에 이러한 노이즈들을 제거해야 합니다. 그렇지 않으면 DBSCAN에서 처럼 하나의 노이즈 point가 두 클러스터를 연결하는 브릿지 역할을 하여 의도치 않게 한 클러스터로 합쳐지게 될 수 있기 때문입니다. HDBSCAN 에서는 이러한 노이즈들을 “해수면을 낮추는” 방식으로 제외합니다. 여기서 밀도가 높은 부분을 육지라고 한다면 밀도가 작은 부분은 바다가 될 것입니다. 그렇다면 어떻게 노이즈를 제외할 수 있을까요? 우선 mutual reachability distance라는 것을 이해해야 합니다.

Core distance
- $core_k(a)$ : point a에서 k개의 이웃을 포함하는 최소의 radius
Mutual reachability distance
- $d_{mreach-k}(a,b) = max(core_k(a), core_k(b), d(a, b))$
- d(a, b) : a와 b사이의 거리

위 $d_{mreach-k}(a,b)$ 의 값을 생각해보면 밀도가 높은 부분에서는 두 점 사이의 거리인 d(a, b)값을 갖게 되는 경우가 대부분일 것입니다. 하지만, 밀도가 낮은 부분에서는 실제 두 점 사이의 거리보다 더 큰 core distance값을 갖게 될 것입니다. 이는 다시 말하면 밀도가 높은 육지 부분은 그대로 둔 채로 밀도가 낮은 바다 부분은 더욱 sparse하게 펼쳐 줄 것입니다. 이러한 방식으로 “해수면을 낮추는” 작업(바다 지점을 육지에서 더 멀리 만드는 작업)을 수행하게 됩니다. 여기서 k는 hyper-parameter로 보통 MinPts과 동일하게 설정합니다.

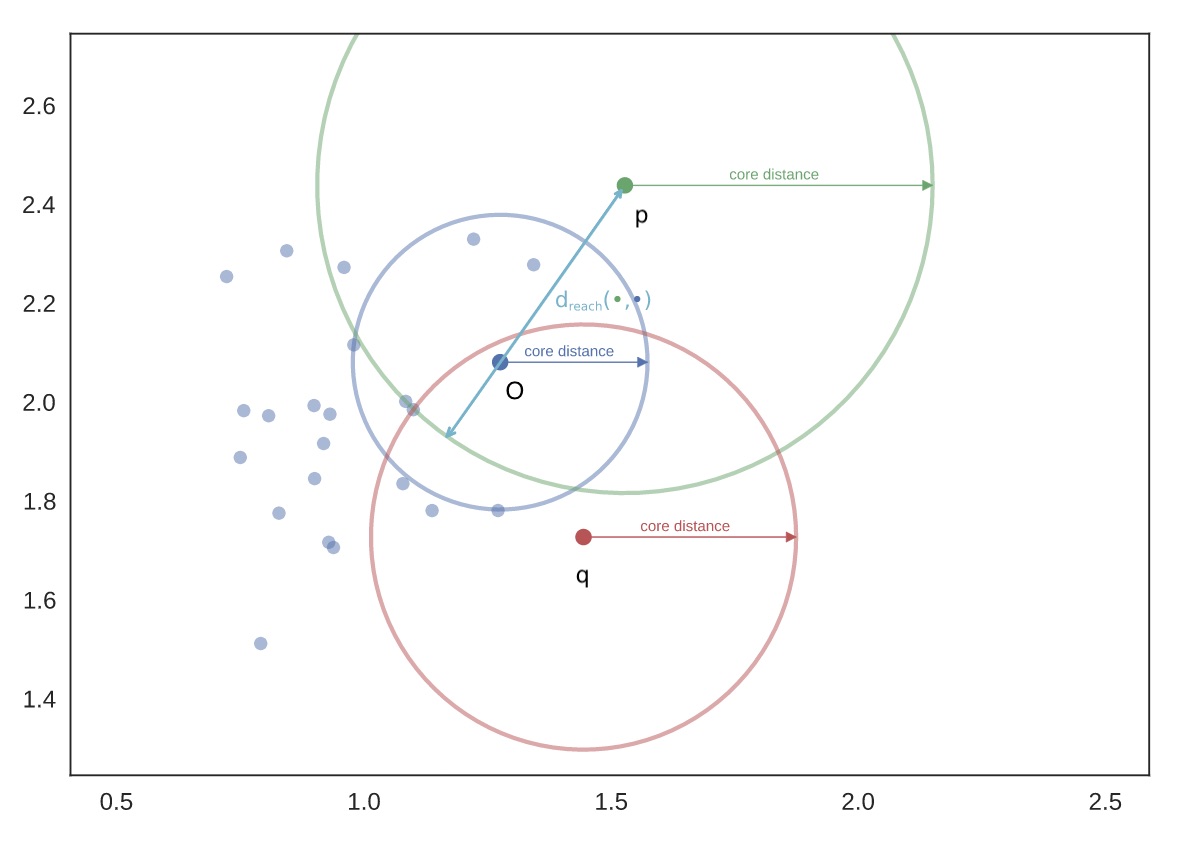
core distance 개념

위 그림에서 $d_{mreach-k}(o,p) = core_k(p)$ 이며, $d_{mreach-k}(o,q) = core_k(q)$ 가 됩니다. 즉, sparse한 영역의 point들은 더욱더 멀리 밀어내게 됩니다. 따라서 해당 단계에서는 각 point간의 distance를 계산하여 모든 $d_{mreach-k}$를 구해야 합니다.

2. MST 생성

이제 우리는 밀도가 높은 cluster를 찾기 위해 모든 point 간의 $d_{mreach-k}(p, q)$ dataset을 얻었습니다. 물론 밀도는 상대적이며 서로 다른 cluster는 서로 다른 밀도를 가질 수 있습니다. 이 dataset에서 data point를 vertex로 $d_{mreach-k}(p, q)$를 edge로 하여 weighted graph를 구성합니다. 적절히 높은 threshold 값을 설정한 뒤 점점 낮춰 가면서 해당 값보다 높은 가중치의 edge들을 제거해 갑니다. 결국 우리는 graph안의 connected component들의 hierarchy를 얻게 될 것입니다. 여기서 MST를 구하는 비용이 brute force로 하면 $O(|V|⋅|E|)$로 상당히 크지만 널리 알려진 Prim’s 알고리듬을 사용하면 $O(|E|⋅log|V|)$ 로 줄일 수 있습니다. 해당 알고리듬은 graph의 모든 노드들을 순회하며 lowest weight 순으로 edge를 추가합니다. 결국 아래 그림처럼 MST를 만들어 줍니다.

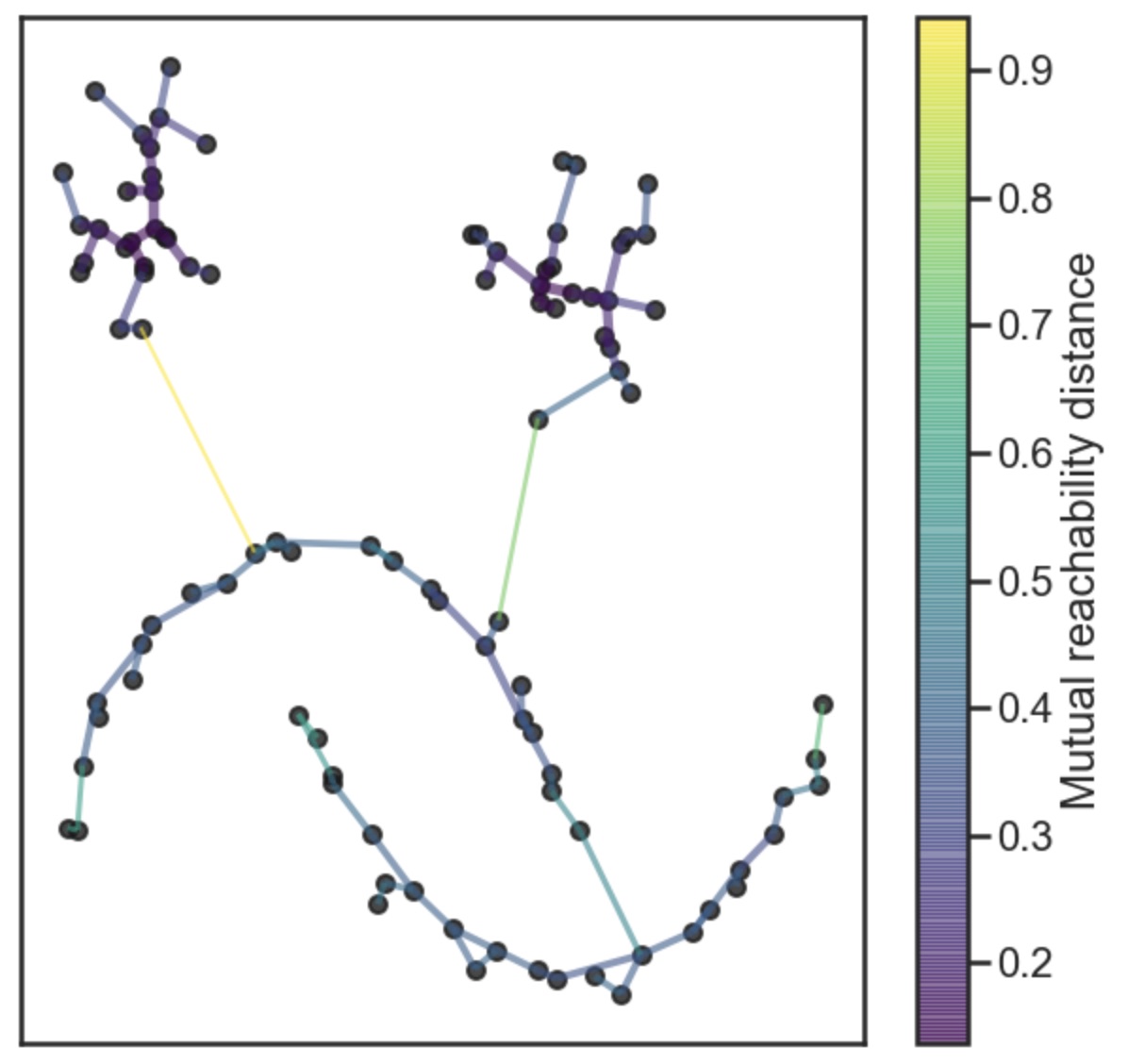
Sample dataset에 대한 MST 결과

아래 코드는 Prim’s 알고리듬의 python example 코드 입니다.

from heapq import heappop, heappush

#
# Prim's algorithm
#
def prim(g):
  tot_cost = 0
  explored = set()
  start = next(iter(g))
  unexplored = [(0, start)]
  while unexplored:
    c, winner = heappop(unexplored)
    if winner not in explored:
      explored.add(winner)
      tot_cost += c
      for nb, cost in g[winner]:
        heappush(unexplored, (cost, nb))
  return tot_cost, explored

# key: src vertex, value: [[dest vertex, weight], ...]
graph = {
  'A': [['B',1], ['D',2], ['F',9]],
  'B': [['A',1], ['C',2], ['D',3], ['F',1]],
  'C': [['B',2], ['E',5]],
  'D': [['A',2], ['B',3], ['E',4]],
  'E': [['C',5], ['D',4], ['F',5]],
  'F': [['A',9], ['B',1], ['E',5]],
}

print('graph = {}'.format(graph))
cost, mst = prim(graph)
print(' cost : {}\n mst : {}'.format(cost, mst))

3. Cluster hierarchy 구축

MST가 주어지면, 다음 단계는 이를 connected component들의 계층 구조로 변환하는 것입니다. 이것은 MST에서 distance가 작은 edge 부터 순회하며 새로운 클러스터에 합쳐주면 얻을 수 있습니다. 해당 edge를 어느 클러스터에 포함시켜 줄지 선정하는 작업이 어려운 부분인데, 이는 다소 아름다운 union-find 알고리듬을 이용하면 효과적으로 처리 가능합니다. 이런 아름다운 알고리듬 덕분에 우리 인간들이 화성을 탐사하고 인류 문명이 발전 할 수 있었다는 것을 생각한다면 마음이 경건해집니다. 아래 그림은 모든 edge들을 순차적으로 결합시킨 connected component의 계층 구조를 보여줍니다.

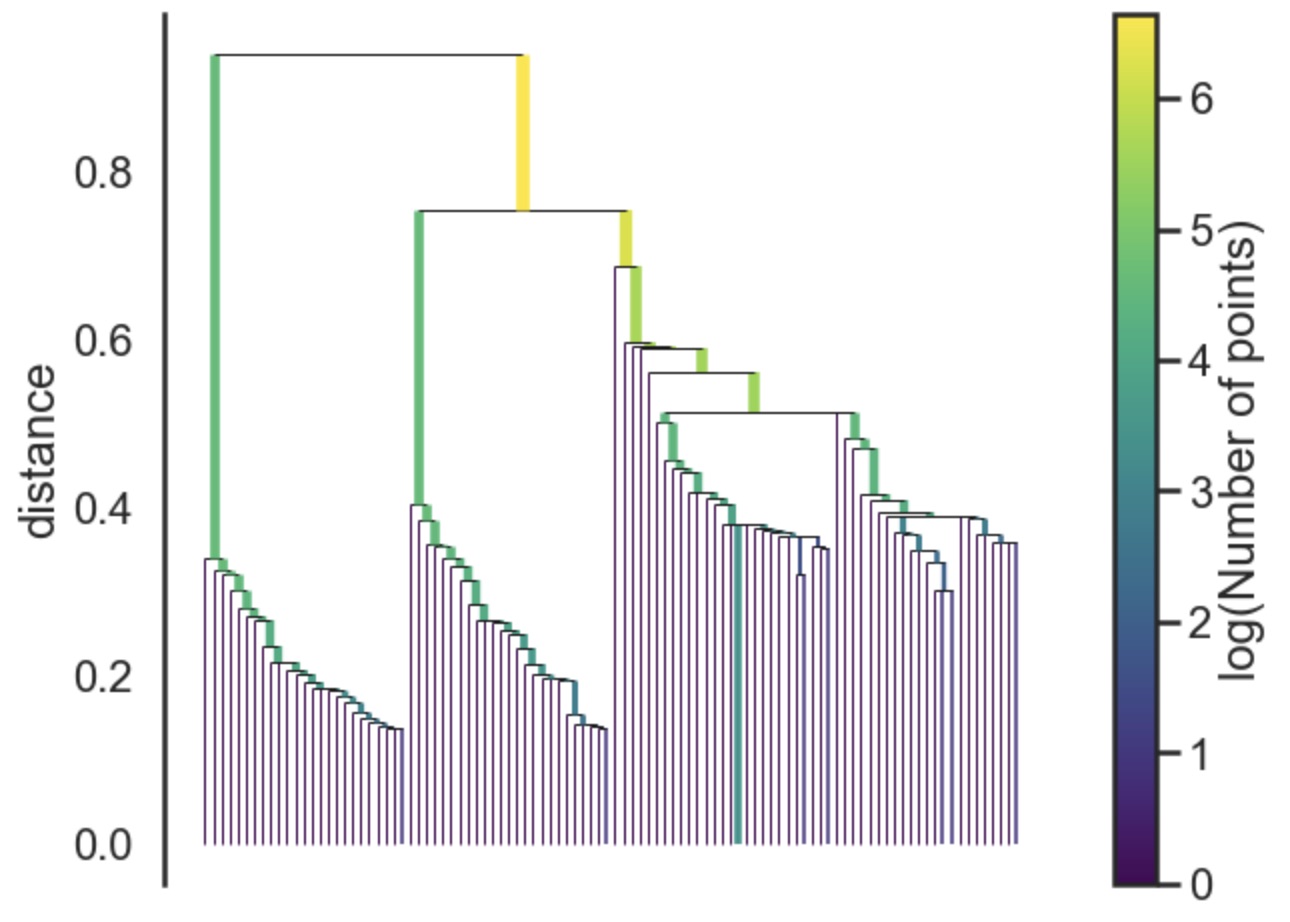
Sample dataset에 대한 cluster 계층 트리 결과

아래 코드는 Union-find 알고리듬의 python example 코드입니다.

import collections

#
# Union-find data structure
#

# 같은 cluster에 포함된 부모 정보 저장
parent = {}
# cluster의 size 정보 저장
cluster_size = collections.defaultdict(lambda:1)

# 초기화 함수
def init_unionfind(vs):
  # 부모가 자신이 되도록 초기화
  for v in vs:
    parent[v] = v

# 해당 노드가 포함된 cluster의 root 노드 정보 return
def find(x):
  # find 연산 비용을 줄이기 위해 parent의 parent 정보 setting
  while parent[x] != x:
    parent[x] = parent[parent[x]]
    x = parent[x]
  return x

# 두 노드가 포함된 cluster를 merge 하는 함수
def union(x, y):
  r1 = find(x)
  r2 = find(y)
  # size가 작은 cluster를 큰 cluster로 merge 한다.
  if cluster_size[r1] > cluster_size[r2]:
    cluster_size[r1] += cluster_size[r2]
    parent[r2] = r1
  else:
    cluster_size[r2] += cluster_size[r1]
    parent[r1] = r2

클러스터 계층 구조도 좋지만 우리는 결국 flat한 클러스터 결과 집합을 알고 싶습니다. DBSCAN의 경우 위 다이어그램을 특정 distance에서 수평선을 그려 잘려진 부분을 독립된 클러스터로 선언합니다. DBSCAN은 이 부분을 hyper-parameter로 남겨 둡니다. 하지만, 각 클러스터마다 density가 다를 수 있기 때문에 global하게 수평선을 그려 잘라낸다면 이상적인 클러스터 모양이 나오긴 힘들 것 입니다. 다음 단계에서 이 부분에 대한 개선이 이루어집니다.

4. Condense the cluster tree

이 단계에서는 복잡한 클러스터 계층 tree를 단순하게 압축 시켜 줍니다. 위 connected component의 계층 구조 그림에서 보았듯이 tree를 따라 내려가 보면 대부분 한 두개의 노드가 클러스터에서 분리 되는 경우가 대부분임을 알 수 있습니다. 이런 경우 하나의 클러스터가 두개로 나눠진다라고 하기 보다는 그저 같은 클러스터에서 노드 하나가 떨어져 나갔다라고 보는것이 적절할 것입니다. 하지만 한두개가 아닌 다수의 노드들이 떨어져 나가는 경우라면 클러스터가 두개로 분리되었다라고 보는것이 맞을 것 입니다. 여기서 MinPts hyper-parameter가 사용됩니다. 정리하면 다음과 같은 조건으로 tree를 축약하여 단순한 tree로 만들어 줍니다.

Breadth_First_Traversal(node):
  if node.left_cnt >= MinPts and node.right_cnt >= MinPts:
    left child와 right child에 각각 새로운 cluster 할당
  else:
    부모의 cluster에 포함됨

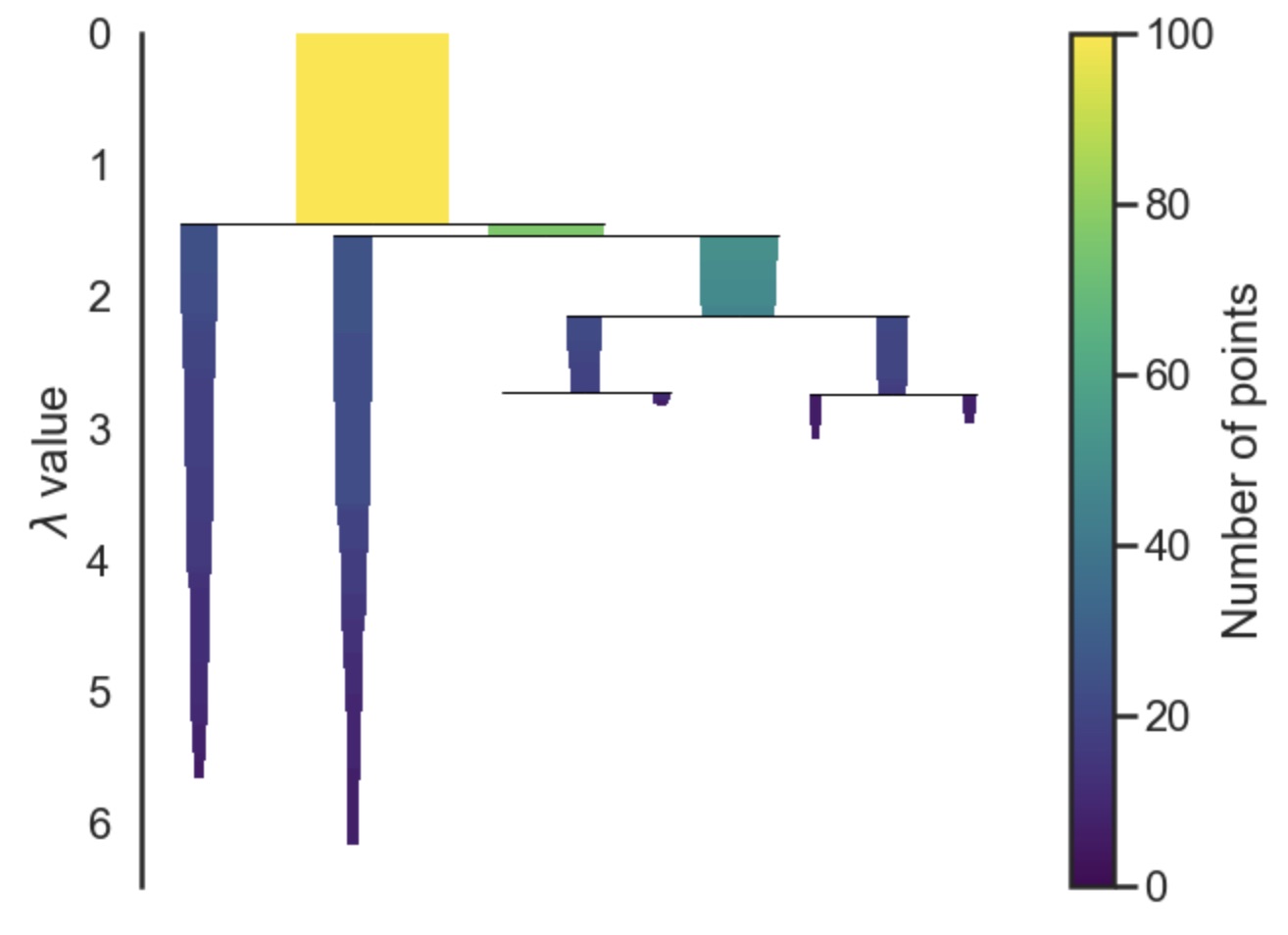
Sample dataset에 대한 압축된 cluster 계층 트리 결과

$\lambda$ 값은 다음에 정의 됩니다.

5. Extract the clusters

마지막으로 우리는 좀 더 persistent(stable)한 클러스터를 선택 해야 합니다. 그리고 만약 부모 클러스터가 선택되었다면 해당 자식 클러스터는 선택에서 제외되게 됩니다. 클러스터에 포함된 노드들의 persistence는 아래와 같은 수식으로 표현됩니다.

$\lambda = \frac{1}{distance}$

물론 여기서의 distance는 mutual reachability distance를 가리킵니다. 각 클러스터마다 생성될 당시의 $\lambda_{birth}$ 값을 가지고 클러스터 전체에 대한 persistence(stability) 를 아래와 같이 계산할 수 있습니다.

$C_{stability}^i = \sum_{p\in cluster_i}(\lambda_p - \lambda_{birth}^i)$

이제 우리는 클러스터마다의 $C_{stability}^i$ 값을 토대로 최종 클러스터를 선택하면 됩니다. 선택 조건은 아래와 같습니다.

모든 leaf component를 독립된 클러스터로 선택합니다.

Connected component의 계층 tree를 DFS로 순회합니다:
  if 두 자식 클러스터의 stability값의 합이 자신의 stability 값보다 크다면:
    자신의 stability 값을 자식 클러스터들의 stability 합으로 assign 합니다
  elif 자신의 stability 값이 더 크다면:
    현재(자신) 클러스터를 선택합니다
    현재 클러스터가 선택되면 자식 클러스터들은 모두 선택에서 제외됩니다

아래 그림은 stability값을 토대로 최종 선택된 클러스터를 보여줍니다.

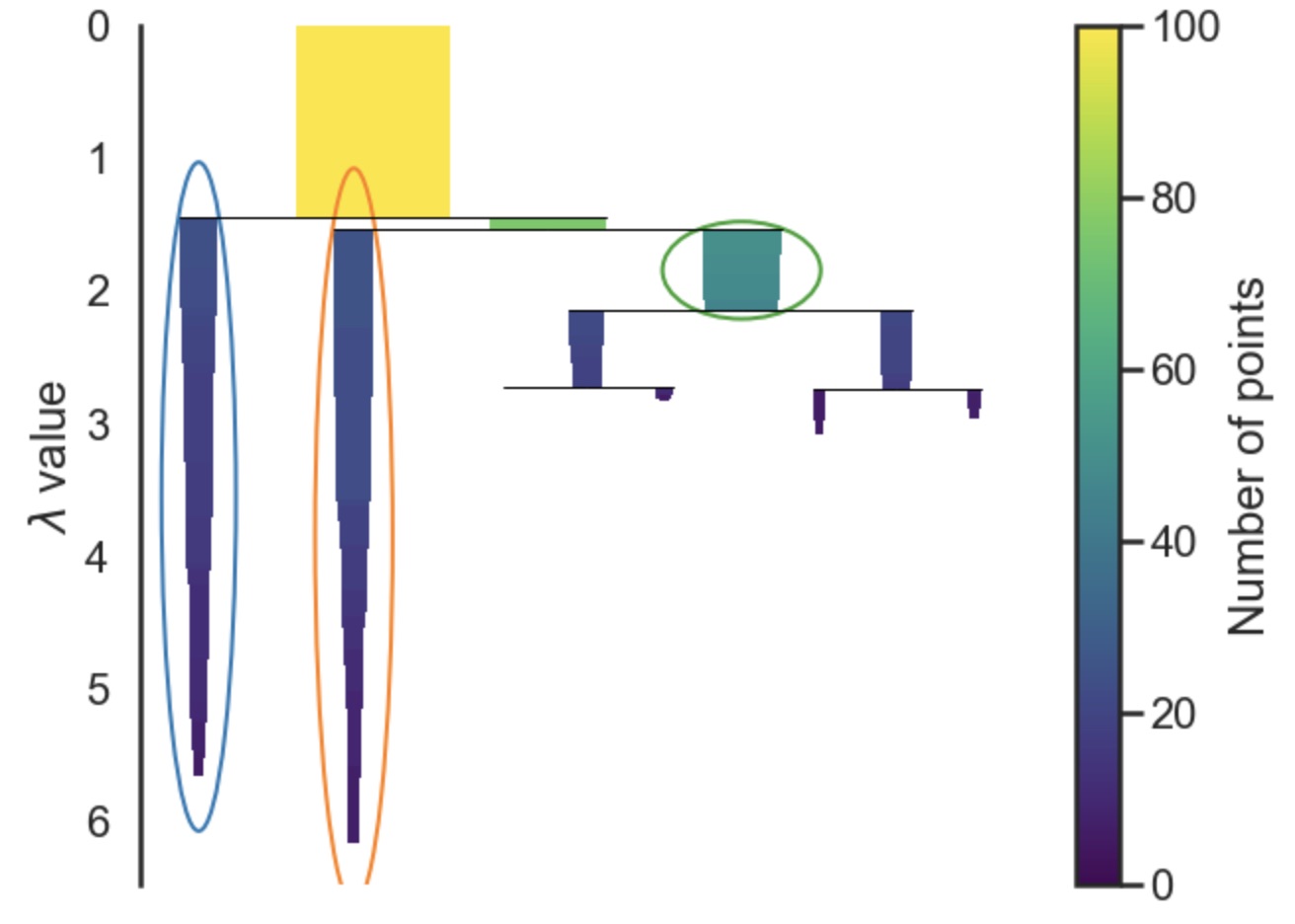
cluster 계층 트리에서 선택된 클러스터 결과

또한 아래 그림은 각 point에 대한 소속 클러스터를 색깔로 보여줍니다. 여기서 색깔의 명암은 normalized된 $\lambda_p$값을 가지고 계산되었습니다.

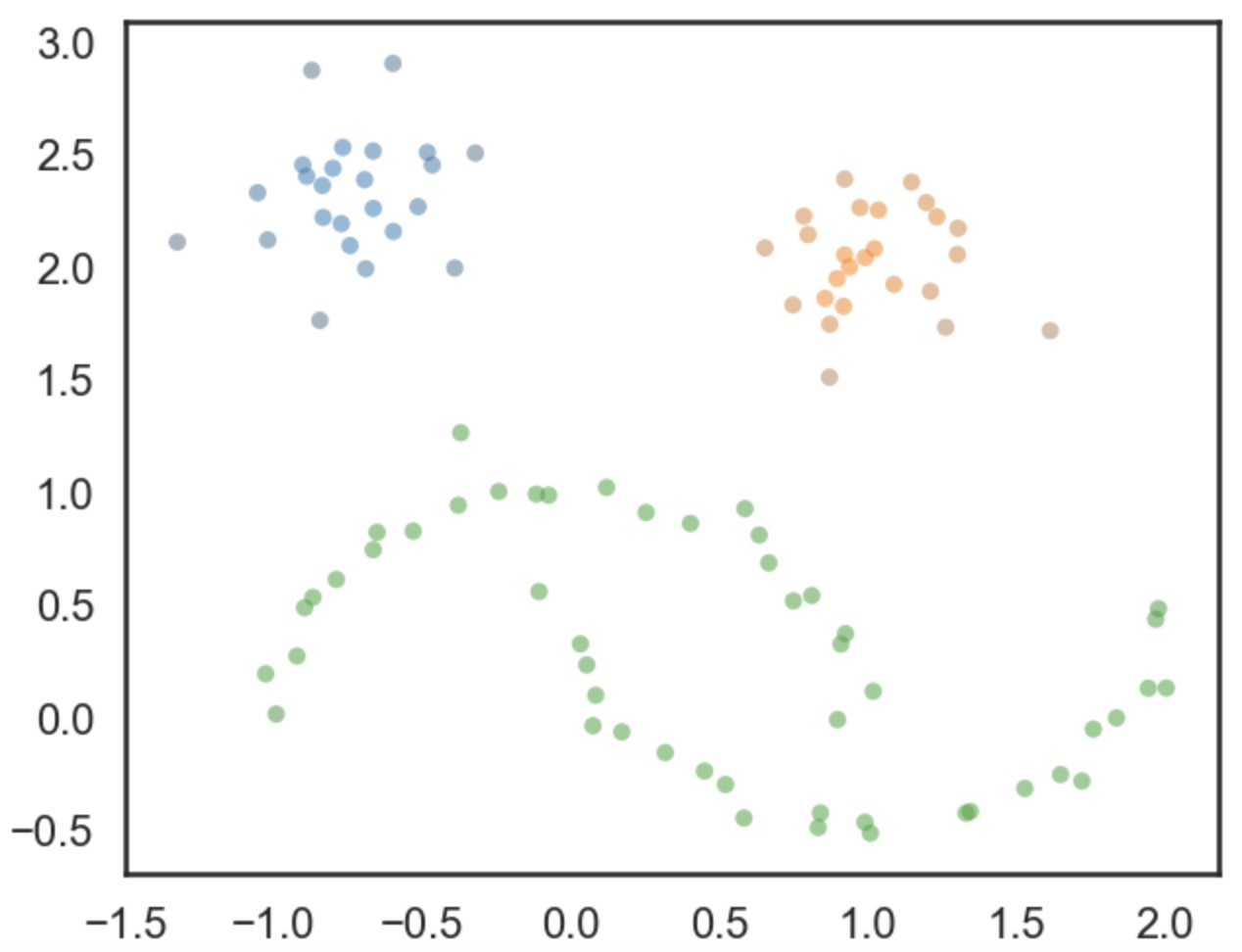
모든 point에 대한 클러스터 할당 결과

끝으로 2020년이 지나가기 전에 semi-supervised/unsupervised 학습에서도 혁신적인 발전이 이루어졌으면 하는 필자의 바람을 끝으로 포스트를 마칩니다. 다음 시간에는 매우 큰 dimension에서도 clustering을 효과적으로 처리할 수 있는 deep learning 기반의 clustering 기법에 대해 설명드리겠습니다~

Reference

Hdbscan: https://arxiv.org/pdf/1705.07321v2.pdf
Hierarchical Clustering: https://arxiv.org/pdf/1506.06422v2.pdf
http://cseweb.ucsd.edu/~dasgupta/papers/tree.pdf
Open source: https://github.com/scikit-learn-contrib/hdbscan