Time-series 데이터 분석: Holt-Winters

우리는 종종 시계열 데이터에 대한 분석/예측을 하게 됩니다. 예를 들어 다음 시간의 주가를 예측하거나, 며칠 후의 매출을 예측하거나, 내일의 기온을 예측하는 일이 이에 해당합니다. 아래와 같이 시계열 데이터를 분석하는 방법들은 상당히 다양합니다.

AR
MA
ARIMA
VAR
VARMA
Simple Exponential Smoothing
Holt-Winters
…

오늘은 이 중에서도 이론적으로 복잡하지 않으면서 상당히 효과적으로 예측을 하는 Holt-Winters 방법을 알아보도록 하겠습니다.

$x_{n+h}^n$ 을 time n 까지의 관측된 데이터를 가지고 예측한 n + h 시점에 대한 x값이라고 나타내 봅시다.
즉, n 은 실제 데이터를 포함하는 trainset 에 해당하는 마지막 시간을 나타내며, n + h 는 예측하고자 하는 미래 시간을 나타냅니다.

h = 1 이라고 한다면, 우리는 아래와 같은 몇몇 naive 한 방법으로도 예측할 수 있습니다.

$x_{n+1}^n = x_n$
$x_{n+1}^n = x_{n+1-S}$ , 예를 들어 S = 7 (weekly seasonal 값)
$x_{n+1}^n = \frac{\sum_{i=1}^{n}x_i}{n}$

하지만 늘 그렇듯이 우리는 좀 더 아름다운 방법을 원합니다.
학부 때 배운 geometric series 를 활용하여 좀 더 아름답게 개선해 보겠습니다.

$\sum_{k=0}^{\infty}(1-\alpha)^k = \frac{1}{\alpha}$, for $0<\alpha<2$

이를 풀어서 다시 써보면,

$\sum_{k=0}^{\infty}(1-\alpha)^k = 1 = \alpha + \alpha(1-\alpha)+\alpha(1-\alpha)^2+\cdots+\alpha(1-\alpha)^k+\cdots$

가 됩니다.

이처럼 sum 이 1이 되는 decaying series를 가중치로 사용하게 된다면, 시간이 가까운 데이터는 가중치를 높게 할당하고 오래전 데이터는 가중치를 작게 할당하여 미래의 x값을 예측할 수 있게 됩니다. 이를 exponential smoothing 이라고 부릅니다.

$x_{n+1}^n = \alpha x_n + \alpha(1-\alpha) x_{n-1} + \alpha(1-\alpha)^2 x_{n-2}+\cdots+\alpha(1-\alpha)^k x_{n-k}+\cdots \tag{1}$

위 수식(1)을 좀 더 간결하고 아름답게 recurrence form으로 표현하기 위해 $(1-\alpha)$를 곱하고 n을 n + 1 로 치환시켜주면 아래와 같은 수식을 얻게 됩니다.

$x_{n+1}^n = \alpha x_n + (1-\alpha)x_{n}^{n-1}$

초기 조건을 $x_2^1 = x_1$ 이라고 가정 한 뒤 n을 증가시켜가며 풀어보면 아래와 같습니다.

$x_2^1 = x_1$
$x_3^2 = \alpha x_2 + (1-\alpha)x^1_2$
$x_4^3 = \alpha x_3 + (1-\alpha)x^2_3$
…

즉, n + 1 시간의 새로운 예측 값이란 $\alpha \times (n$ 시간의 실측 값$) + (1-\alpha)\times(n$ 시간의 예측 값$)$
이 되게 됩니다.

그렇다면, 어떻게 적절한 $\alpha$ 값을 구할 수 있을까요? 그것은 단순히 예측값들과 실측값들에 대한 sum of squared errors(SSE)를 가지고 구할 수 있습니다.

$SSE(\alpha) = \sum_{i=1}^{n}(x_n - x_n^{n-1})^2$

$\alpha_{opti} = argmin_{\alpha}SSE(\alpha)$

이제 위 알고리듬을 Holt-Winters 방법으로 확장 시켜 보겠습니다.
Holt-Winters 알고리듬은 단순한 exponential smoothing 뿐만 아니라 trend 속성과 seasonality 속성이 추가되게 됩니다.

여기서 trend란 장기적인 데이터의 경향을 나타내며, seasonality란 데이터의 반복되는 주기성을 나타내게 됩니다. 따라서 trend 개념은 n + 1 시간의 값과 n 시간의 값의 차이이며, 이를 나중에 exponential smoothing 하게 됩니다.

일단 trend term을 추가하여 예측을 새롭게 정의해 보겠습니다.

$\hat{x}_{n+1} = level_n + trend_n$

여기서 ^를 사용하여 n + 1 시점의 예측값을 나타냈으며, $level_n$ 은 n시점에 예측된 n + 1 시점의 level 값을 나타냅니다.

일단 trend는 무시하고 level을 앞에서 설명했던 exponential smoothing 으로 다음처럼 표현해봅시다.

new level = $\alpha \times$ new information $+ (1 - \alpha) \times $ old level

\[\hat{x}_{n+1} = \alpha x_n + (1-\alpha)\hat{x}_n \xrightarrow[ ]{\hat{x}_{n+1}=level_n} level_n = \alpha x_n+(1-\alpha)level_{n-1}\]

그런 다음 장기적인 데이터의 경향 정보를 포함하는 trend를 고려하여 new level을 예측할 때 old level 값뿐만 아니라 trend 값을 포함시켜 봅시다.

new level = $\alpha \times$ new information $+ (1 - \alpha) \times ($ old level + old trend $)$

따라서 아래와 같은 수식을 얻게 됩니다.

\[level_n = \alpha x_n+(1-\alpha)(level_{n-1} + trend_{n-1})\]

trend 또한 $\beta$ 라는 파라미터를 사용하여 exponential smoothing 하여 나타내 봅니다.

$trend_n = \beta \times$ new trend $+ (1-\beta) \times$ old trend
$\rightarrow$
$trend_n = \beta(level_n-level_{n-1})+(1-\beta)trend_{n-1}$

또한, 초깃값은 아래와 같습니다.
$level_1=x_1$
$trend_1=x_2-x_1$

$\beta_{opti}$ 값 또한 $\alpha_{opti}$처럼 SSE가 최소가 되는 지점을 찾아 구할 수 있습니다.

이제 seasonality term을 추가해 보겠습니다. Seasonality란 앞에서 말했던 것처럼 데이터의 주기성 정보를 포함하게 됩니다. 이 반복되는 short-term 패턴은 보통 아래 그림처럼 multiplicative와 additive 두 가지 타입으로 나눌 수 있습니다.

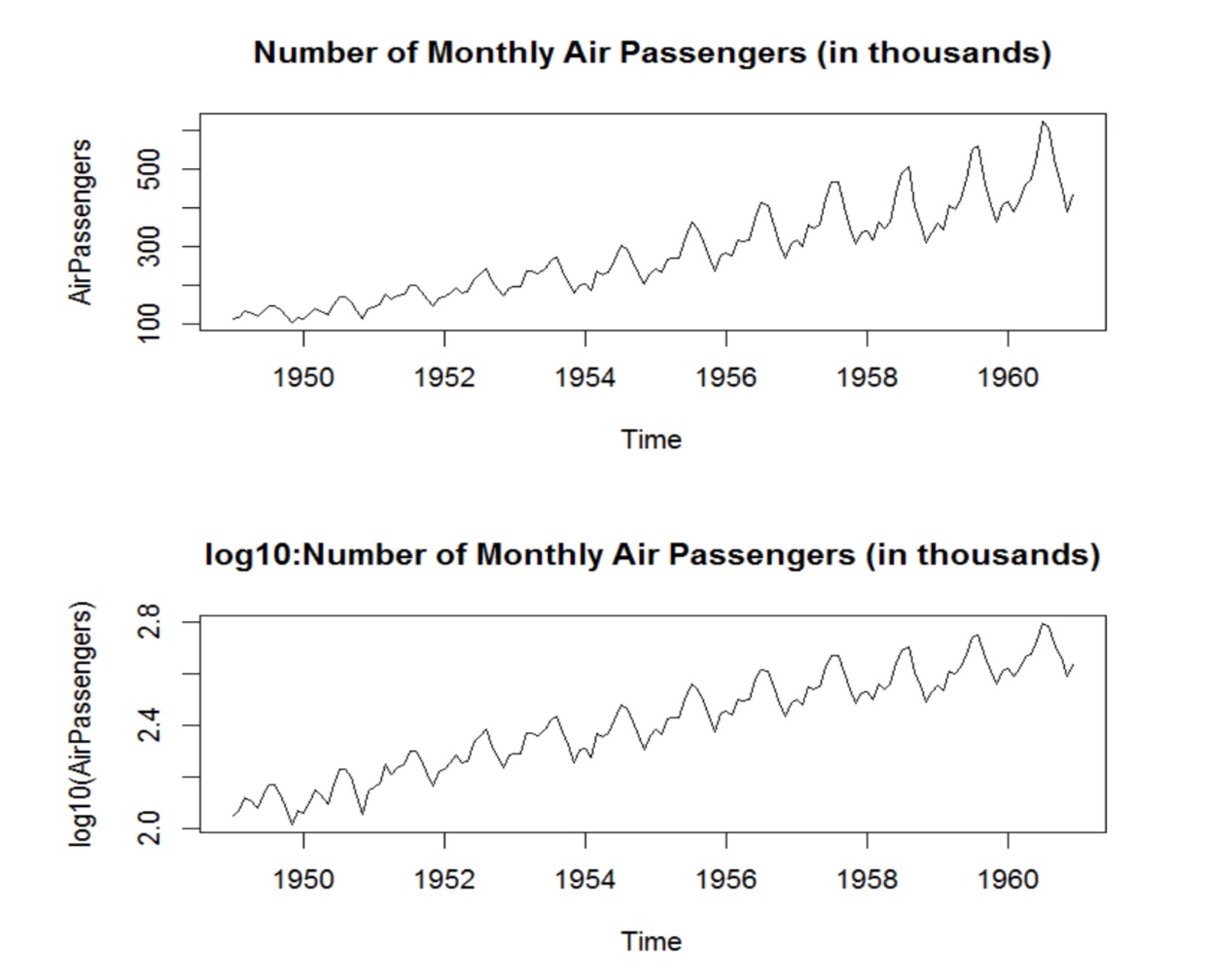
seasonality-type

첫 번째 그림은 multiplicative 특징을 보여주며, 두 번째 그림은 additive 특징을 보여줍니다.

일단 앞에서 trend term을 추가하였던 것처럼, 시간 주기가 m인 seasonality term을 추가해 보면 h시간 후의 예측값 $\hat{x}_{n+h}$ 은 아래와 같이 표현됩니다.

for additive type: $\hat{x}_{n+h}=level_n + h \times trend_n + seasonal_{n+h-m}$
for multiplicative type: $\hat{x}_{n+h}=(level_n + h \times trend_n) \times seasonal_{n+h-m}$

m값의 경우 만약 시간 unit이 day이고 weekly seasonal(7 days)을 가정하면 m = 7이 됩니다.

각 term 들을 정리해 보면 아래와 같습니다.

\[level_n = \alpha(x_n - seasonal_{n-m}) + (1-\alpha)(level_{n-1}+trend_{n-1})\] \[trend_n = \beta(level_n - level_{n-1}) + (1-\beta)trend_{n-1}\] \[seasonal_n = \gamma(x_n - level_n)+(1-\gamma)seasonal_{n-m}\]

마지막으로 $\alpha_{opti}, \beta_{opti}, \gamma_{opti}$ 값을 구하려면 SSE가 최소가 되는 지점을 찾아 구하면 됩니다.

이를 Holt-winters 알고리듬이라고 하며 직접 구현해도 괜찮지만, 굳이 그럴 필요없이 statsmodels library를 이용하면 더 쉽게 구현이 가능합니다.

아래는 다음 시간의 CTR을 예측하는 python code example을 보여줍니다.

import pandas as pd
from statsmodels.tsa.api import ExponentialSmoothing

SELECT_QUERY = '''...read dataset query...'''
dataset = pd.read_sql(SELECT_QUERY, db)

dataset.index = dataset.local_time
dataset = dataset.reindex(pd.DatetimeIndex(start=dataset.index[0], end=last_date, freq='D'))
dataset.fillna(0., inplace=True)

fit_exp = ExponentialSmoothing(dataset.expose_cnt, seasonal_periods=7, trend=None, seasonal='add').fit(use_boxcox=False)
# last_date
forecast_exp = fit_exp.forecast(1)

fit_click = ExponentialSmoothing(dataset.click_cnt, seasonal_periods=7, trend=None, seasonal='add').fit(use_boxcox=False)
# last_date
forecast_click = fit_click.forecast(1)

forecast_ctr = forecast_click.values[0]/forecast_exp.values[0]

다음 시간에는 time-series 데이터 예측에서 많이 사용되는 ARIMA에 대해서 알아보도록 하겠습니다~