Quantum Computer

안녕하세요. 오태호입니다.

우리는 Computer Program을 개발할 때 깊은 수준의 물리학을 알아야 될 필요는 없이 Computer Program의 개발에 필요한 수준의 Computer 작동 원리만을 이해하고 개발을 합니다. 마찬가지로 Quantum Computer Program을 개발할 때도 깊은 수준의 물리학을 알아야 될 필요 없이 Quantum Computer Program의 개발에 필요한 수준의 Quantum Computer의 작동 원리만을 이해하고 개발을 하면 됩니다. 이번 글에서는 Quantum Computer를 사용하기 위해 기본적으로 알아야 되는 내용을 정리해 보았습니다. 이 글에 있는 내용만으로 Quantum Computer Program의 개발을 하는 것은 무리가 있겠지만, 일단 이 글의 내용을 이해하고 나면 다른 Quantum Computer Program의 개발에 대한 자료를 이해하는데 많은 도움이 될 것으로 생각합니다.

이 글을 이해하기 위해서 대학 수준의 Calculus, Linear Algebra, Complex Number에 대한 기초지식이 필요합니다. Computer Science에서 배우는 Digital Logic에 대한 내용을 이해하고 있으면 이 글을 이해하는데 다소 도움이 되지만 해당 지식이 없어도 이 글을 이해하는데 큰 문제는 없습니다.

Quantum Computer를 직접 제조하기 위해서는 Computer를 직접 제조하는 것과 마찬가지로 상당히 깊은 수준의 물리학 지식이 필요합니다. 이 글에서는 Quantum Computer의 사용에 필요한 내용만을 다루고 제조에 대한 내용은 다루지 않습니다.

Complex Number

다음과 같은 Complex Number가 있다고 합시다.

\[c=a+ib\]

$c$의 Absolute Value(Modulus 혹은 Magnitude라고도 함)는 다음과 같이 정의합니다.

\[|c|=\sqrt{a^2+b^2}\]

$c$는 Argument(Phase라고도 함)가 $\phi$일 때 다음과 같이 표현할 수도 있습니다.

\[c=|c|e^{i\phi}=|c|(\cos{\phi}+i\sin{\phi})\]

Qubit

1Qubit는 수식으로 다음과 같이 표현합니다.

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\]

$c_0$와 $c_1$은 Complex Number입니다.

해당 Qubit가 $0$이라면 $c_0=1$, $c_1=0$이 되고, 해당 Qubit가 $1$이라면 $c_0=0$, $c_1=1$이 됩니다.

Qubit는 내용을 읽으면 State Collapse가 발생하여 $0$($c_0=1$, $c_1=0$)으로 변하거나 $1$($c_0=0$, $c_1=1$)으로 변하고 원래의 State($c_0$, $c_1$)를 복구할 수 없습니다.

Qubit를 읽을 때 Qubit가 $0$이 될 확률은 $|c_0|^2$이고 Qubit가 $1$이 될 확률은 $|c_1|^2$입니다. Qubit는 읽을 때 $0$이나 $1$이 되어야 되기 때문에 $|c_0|^2+|c_1|^2=1$이 됩니다.

결국 위에서 언급한 1Qubit의 수식은 Qubit가 가지고 있는 State를 표현하고 Qubit를 읽을 때 $0$이 될 확률과 $1$이 될 확률을 표현합니다. $|c_0|^2+|c_1|^2=1$이기 때문에 $c_0$만 알면 $c_1$을 알 수 있을 것 같지만 $c_0$와 $c_1$이 둘 다 Complex Number이기 때문에 $c_0$을 알고 있어도 이를 만족하는 $c_1$는 무수히 많이 존재합니다. 즉, 1Qubit의 State를 표현하기 위해서는 $c_0$와 $c_1$이 둘 다 필요합니다.

Quantum Logic Gate

Digital Circuit에서는 Digital Logic Gate가 있는 것처럼 Quantum Circuit에서는 Quantum Logic Gate가 있습니다.

Digital Logic Gate는 Bit단위로 Input을 주면 뭔가 변환을 해서 Bit단위로 Output을 내 줍니다. 각 Bit는 $0$ 혹은 $1$의 값을 가집니다. Digital Logic Gate는 AND, OR, NOT, XOR, NAND, NOR, XNOR등이 있습니다. NAND만으로 모든 Digital Logic Gate를 표현할 수 있지만 편의상 여러가지 Digital Logic Gate를 사용합니다.

Quantum Logic Gate는 Qubit단위로 Input을 주면 뭔가 변환을 해서 Qubit단위로 Output을 내 줍니다. 각 Qubit는 $c_0$와 $c_1$의 State의 값을 가집니다. Digital Logic Gate와 마찬가지로 여기서 설명하는 다수의 Quantum Logic Gate들은 소수의 Quantum Logic Gate들만으로 표현이 가능하지만 편의상 여러가지 Quantum Logic Gate를 사용합니다. 여기서는 많이 사용되는 Quantum Logic Gate를 설명합니다. 일부 Quantum Logic Gate는 동일한 기능을 하면서 다른 이름을 가지기도 하는데 그런 것들도 함께 정리하였습니다.

이해를 돕고자 각 Quantum Logic Gate에 수식과 더불어 설명을 적어 놓았는데 설명이 엄밀하게는 따져 보면 맞지 않는 부분이 있습니다. 설명은 이해를 위한 참고만 하고 정확한 작동은 수식을 참고하시기 바랍니다.

NOT

Digital Logic Gate의 NOT Gate와 유사한 Quantum Logic Gate입니다. Digital Logic Gate에는 선 하나가 하나의 값을 가졌지만 Quantum Logic Gate에서는 선 하나가 $c_0$와 $c_1$의 값을 가지는 것에 주의합니다. $c_0$와 $c_1$의 값이 Input으로 주어지면 Quantum Logic Gate가 무언가 변환을 해서 $c_0’$와 $c_1’$이 Output으로 출력됩니다. 이 변환은 Linear Algebra의 Matrix형태로 표현합니다. 즉 Qubit을 읽었을 때 $0$이 될 확률과 $1$이 될 확률에 뭔가 변환을 가합니다. NOT은 Qubit을 읽었을 때 $0$이 될 확률을 $1$이 될 확률로 바꿔주고 $1$이 될 확률을 $0$이 될 확률로 바꿔줍니다. 구체적으로 수식으로 표현하면 다음과 같습니다.

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \end{bmatrix}\] \[q' = c_0' | 0 \rangle + c_1' | 1 \rangle\]

HAD

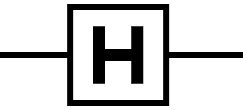
Hadamard라고도 불립니다. Qubit이 $0$이나 $1$일 때 Hadamard를 거치고 나서 해당 Qubit을 읽으면 $0$이 될 확률이 $\frac{1}{2}$이 되고 $1$이 될 확률이 $\frac{1}{2}$이 됩니다. 즉 하나의 Qubit에 $0$과 $1$을 동시에 넣는 것이 가능하며 이것을 Superposition(양자중첩)이라고 부릅니다.

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 & 1 \\ 1 & -1 \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \end{bmatrix}\] \[q' = c_0' | 0 \rangle + c_1' | 1 \rangle\]

PHASE

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & e^{i\phi} \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \end{bmatrix}\] \[q' = c_0' | 0 \rangle + c_1' | 1 \rangle\]

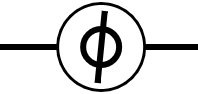
X

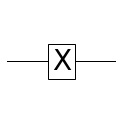
Pauli-X라고도 불립니다. NOT과 동일합니다.

Y

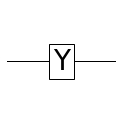
Pauli-Y라고도 불립니다.

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \end{bmatrix} = \begin{bmatrix} 0 & -i \\ i & 0 \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \end{bmatrix}\] \[q' = c_0' | 0 \rangle + c_1' | 1 \rangle\]

Z

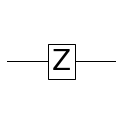
Pauli-Z라고도 불립니다. PHASE($\pi$)와 동일합니다.

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \end{bmatrix}\] \[q' = c_0' | 0 \rangle + c_1' | 1 \rangle\]

S

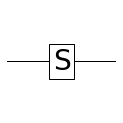
PHASE($\frac{\pi}{2}$)와 동일합니다.

T

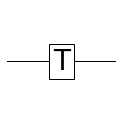
PHASE($\frac{\pi}{4}$)와 동일합니다.

RX

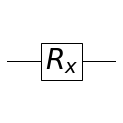
ROTX라고도 불립니다.

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \end{bmatrix} = \begin{bmatrix} \cos(\frac{\theta}{2}) & -i\sin(\frac{\theta}{2}) \\ -i\sin(\frac{\theta}{2}) & \cos(\frac{\theta}{2}) \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \end{bmatrix}\] \[q' = c_0' | 0 \rangle + c_1' | 1 \rangle\]

RY

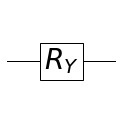
ROTY라고도 불립니다.

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \end{bmatrix} = \begin{bmatrix} \cos(\frac{\theta}{2}) & -\sin(\frac{\theta}{2}) \\ \sin(\frac{\theta}{2}) & \cos(\frac{\theta}{2}) \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \end{bmatrix}\] \[q' = c_0' | 0 \rangle + c_1' | 1 \rangle\]

RZ

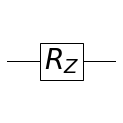
ROTZ라고도 불립니다.

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \end{bmatrix} = \begin{bmatrix} e^{-i\frac{\theta}{2}} & 0 \\ 0 & e^{i\frac{\theta}{2}} \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \end{bmatrix}\] \[q' = c_0' | 0 \rangle + c_1' | 1 \rangle\]

ROOTNOT

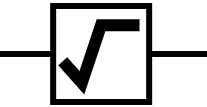
ROOTNOT은 두 번 연속해서 적용하면 NOT이 되는 Quantum Logic Gate입니다.

\[q = c_0 | 0 \rangle + c_1 | 1 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 1+i & 1-i \\ 1-i & 1+i \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \end{bmatrix}\] \[q' = c_0' | 0 \rangle + c_1' | 1 \rangle\]

READ

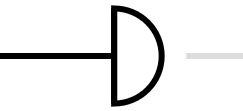
Measure라고도 불립니다. Qubit의 내용을 읽습니다. Qubit는 내용을 읽으면 State Collapse가 발생하여 $0$($c_0=1$, $c_1=0$)으로 변하거나 $1$($c_0=0$, $c_1=1$)으로 변하고 원래의 State($c_0$, $c_1$)를 복구할 수 없습니다.

WRITE

Qubit에 값을 저장합니다. $0$($c_0=1$, $c_1=0$)이나 $1$($c_0=0$, $c_1=1$)로 저장할 수 있습니다.

CNOT

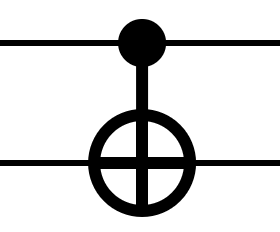
여기서는 Qubit 2개를 동시에 다룹니다. 이전까지는 $0$일 확률에 대한 State인 $c_0$와 $1$일 확률에 대한 State인 $c_1$만 다루었는데 여기서는 Qubit 2개가 $00$일 확률에 대한 State인 $c_0$, $01$(위에서 첫 번째 Qubit이 0, 위에서 두 번째 Qubit이 1)일 확률에 대한 State인 $c_1$, $10$(위에서 첫 번째 Qubit이 1, 위에서 두 번째 Qubit이 0)일 확률에 대한 State인 $c_2$, $11$일 확률에 대한 State인 $c_3$를 다룹니다. Qubit 2개를 읽었을 때 $00$, $01$, $10$, $11$ 중에 한 가지로 될 것이기 때문에 $|c_0|^2+|c_1|^2+|c_2|^2+|c_3|^2=1$이 됩니다.

위에서 첫 번째 Qubit은 그대로 출력합니다. 위에서 첫 번째 Qubit이 1일 때는 위에서 두 번째 Qubit에 NOT을 적용해 주고 그렇지 않은 경우에는 위에서 두 번째 Qubit을 그대로 출력합니다.

\[q = c_0 | 00 \rangle + c_1 | 01 \rangle + c_2 | 10 \rangle + c_3 | 11 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \\ c_2' \\ c_3' \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ c_3 \end{bmatrix}\] \[q' = c_0' | 00 \rangle + c_1' | 01 \rangle + c_2' | 10 \rangle + c_3' | 11 \rangle\]

CCNOT

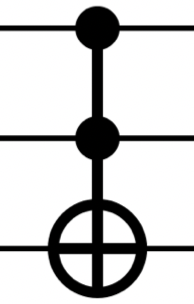
Toffoli라고도 불립니다. CNOT과 유사합니다.

위에서 첫 번째 Qubit과 위에서 두 번째 Qubit은 그대로 출력합니다. 위에서 첫 번째 Qubit이 1이고 위에서 두 번째 Qubit이 1인 경우에는 위에서 세 번째 Qubit에 NOT을 적용해 주고 그렇지 않은 경우에는 위에서 세 번째 Qubit을 그대로 출력합니다.

\[q = c_0 | 000 \rangle + c_1 | 001 \rangle + c_2 | 010 \rangle + c_3 | 011 \rangle + c_4 | 100 \rangle + c_5 | 101 \rangle + c_6 | 110 \rangle + c_7 | 111 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \\ c_2' \\ c_3' \\ c_4' \\ c_5' \\ c_6' \\ c_7' \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ c_6 \\ c_7 \\ \end{bmatrix}\] \[q' = c_0' | 000 \rangle + c_1' | 001 \rangle + c_2' | 010 \rangle + c_3' | 011 \rangle + c_4' | 100 \rangle + c_5' | 101 \rangle + c_6' | 110 \rangle + c_7' | 111 \rangle\]

SWAP

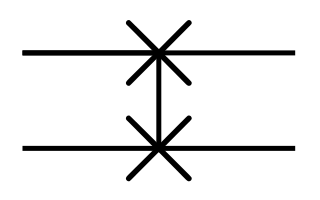
위에서 첫 번째 Qubit과 두 번째 Qubit을 서로 교환합니다.

\[q = c_0 | 00 \rangle + c_1 | 01 \rangle + c_2 | 10 \rangle + c_3 | 11 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \\ c_2' \\ c_3' \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ c_3 \end{bmatrix}\] \[q' = c_0' | 00 \rangle + c_1' | 01 \rangle + c_2' | 10 \rangle + c_3' | 11 \rangle\]

CSWAP

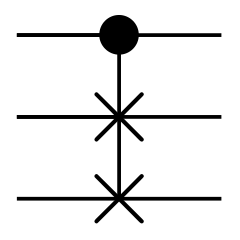
Fredkin라고도 불립니다.

위에서 첫 번째 Qubit은 그대로 출력합니다. 위에서 첫 번째 Qubit이 1일 때 위에서 두 번째 Qubit과 위에서 세 번째 Qubit을 서로 SWAP합니다.

\[q = c_0 | 000 \rangle + c_1 | 001 \rangle + c_2 | 010 \rangle + c_3 | 011 \rangle + c_4 | 100 \rangle + c_5 | 101 \rangle + c_6 | 110 \rangle + c_7 | 111 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \\ c_2' \\ c_3' \\ c_4' \\ c_5' \\ c_6' \\ c_7' \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ c_6 \\ c_7 \\ \end{bmatrix}\] \[q' = c_0' | 000 \rangle + c_1' | 001 \rangle + c_2' | 010 \rangle + c_3' | 011 \rangle + c_4' | 100 \rangle + c_5' | 101 \rangle + c_6' | 110 \rangle + c_7' | 111 \rangle\]

CPHASE

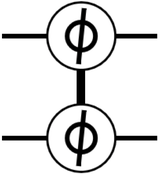
$\phi$에 대한 언급이 없으면 $\pi$를 $\phi$로 사용합니다.

\[q = c_0 | 00 \rangle + c_1 | 01 \rangle + c_2 | 10 \rangle + c_3 | 11 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \\ c_2' \\ c_3' \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e^{i\phi} \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ c_3 \end{bmatrix}\] \[q' = c_0' | 00 \rangle + c_1' | 01 \rangle + c_2' | 10 \rangle + c_3' | 11 \rangle\]

CX

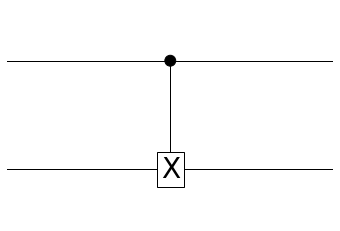
CNOT과 동일합니다.

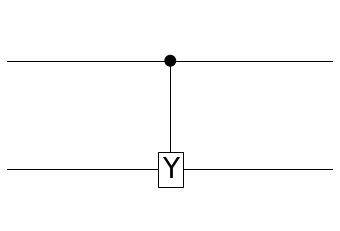
CY

\[q = c_0 | 00 \rangle + c_1 | 01 \rangle + c_2 | 10 \rangle + c_3 | 11 \rangle\] \[\begin{bmatrix} c_0' \\ c_1' \\ c_2' \\ c_3' \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & -i \\ 0 & 0 & i & 0 \end{bmatrix} \begin{bmatrix} c_0 \\ c_1 \\ c_2 \\ c_3 \end{bmatrix}\] \[q' = c_0' | 00 \rangle + c_1' | 01 \rangle + c_2' | 10 \rangle + c_3' | 11 \rangle\]

CZ

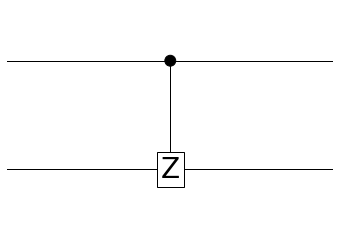
CPHASE와 동일합니다.

Entanglement

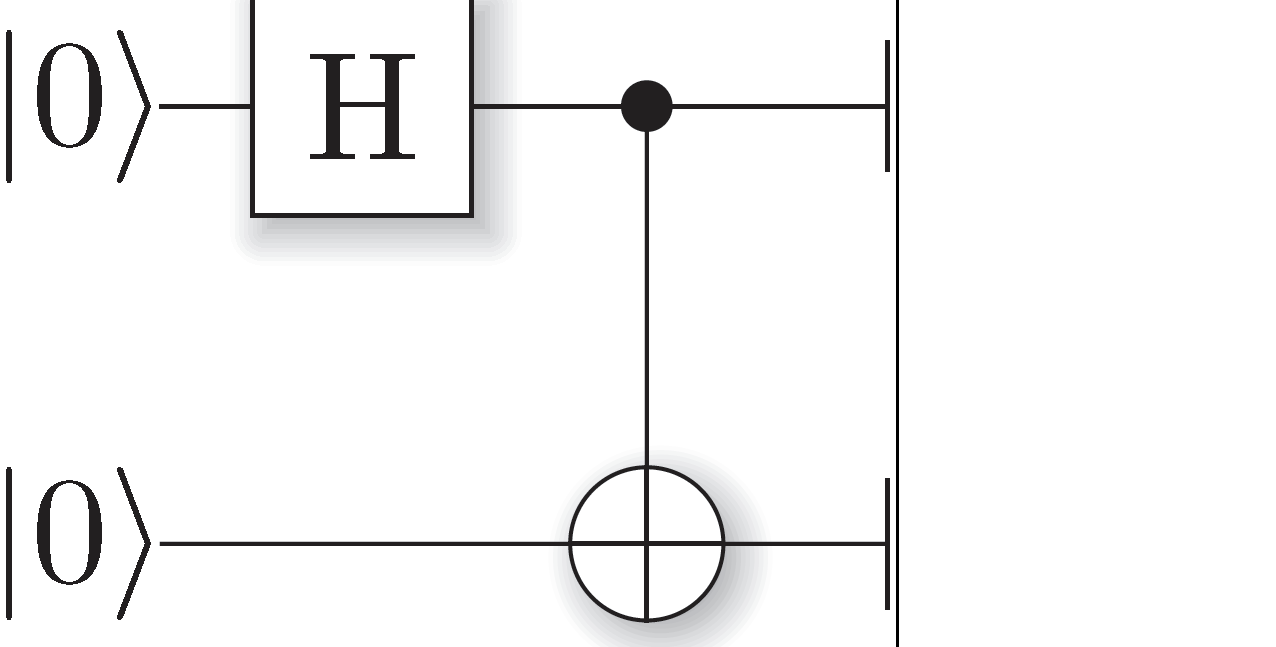
이 Quantum Circuit은 Bell Pairs라고 불리는 Quantum Circuit입니다. Step별로 Qubit을 살펴보겠습니다.

• Step 1

  처음에 두 Qubit를 $00$으로 초기화합니다. 읽었을 때 $00$가 읽힐 확률이 100%입니다.

  \[q = 1 | 00 \rangle\]

• Step 2

  위에서 첫 번째 Qubit에 HAD를 통과시킵니다. 위에서 첫 번째 Qubit가 읽었을 때 $0$이 될 확률이 50%이고 $1$이 될 확률이 50%입니다. 위에서 두 번째 Qubit에는 특별한 처리를 하지 않았기 때문에 읽었을 때 $0$이 될 확률이 100%입니다.

  \[q = \frac{1}{\sqrt{2}} | 00 \rangle + \frac{1}{\sqrt{2}} | 10 \rangle\]

• Step 3

  두 Qubit에 CNOT을 통과시킵니다. 두 Qubit를 읽었을 때 $00$이 읽힐 확률이 50%이고 $11$이 읽힐 확률이 50%가 되었습니다. 즉 두 개의 Qubit가 서로 함께 움직이는 상태가 되었습니다. 이것을 Entanglement(양자얽힘)라고 부릅니다.

  \[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}} \end{bmatrix}\] \[q = \frac{1}{\sqrt{2}} | 00 \rangle + \frac{1}{\sqrt{2}} | 11 \rangle\]

Swap Test

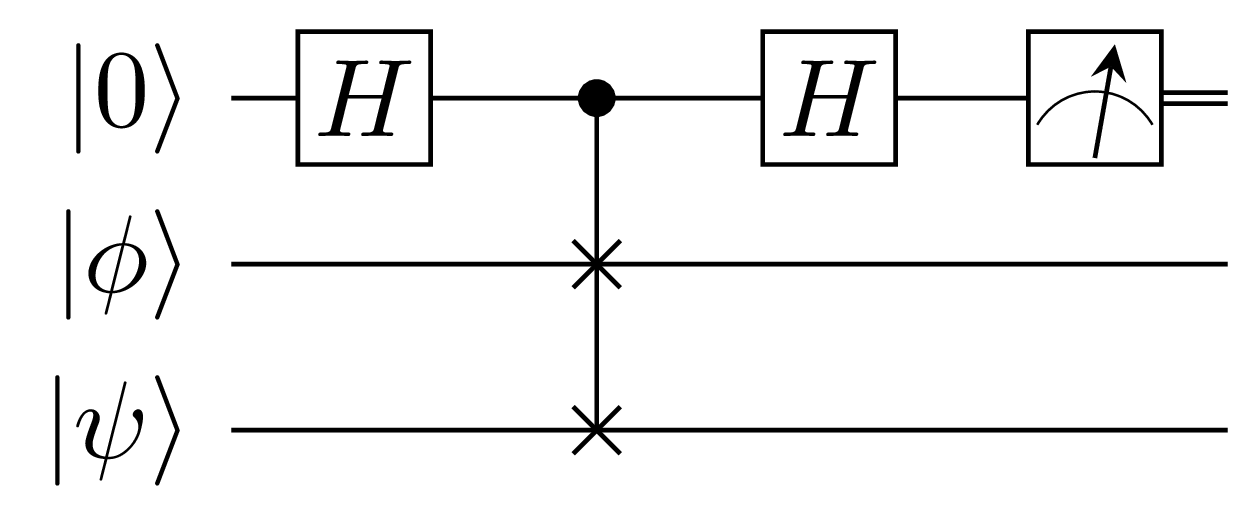
이 Quantum Circuit은 두 Qubit을 비교하는 Quantum Circuit입니다. Step별로 Qubit을 살펴보겠습니다.

• Step 1

  위에서 첫 번째 Qubit은 $0$로 초기화하고 두 번째 Qubit과 세 번째 Qubit을 비교할 예정입니다. 위에서부터 차례대로 $q_0$, $q_1$, $q_2$라 정의하고 각각의 초기 State는 다음과 같이 정의합니다.

  \[q_0 = 1 | 0 \rangle \\ q_1 = c_0 | 0 \rangle + c_1 | 1 \rangle \\ q_2 = d_0 | 0 \rangle + d_1 | 1 \rangle\]

• Step 2

  $q_0$의 초기값을 $0$으로 하고 Qubit전체를 합쳐서 다음과 같이 표현합니다.

  \[q = c_0 d_0 | 000 \rangle + c_0 d_1 | 001 \rangle + c_1 d_0 | 010 \rangle + c_1 d_1 | 011 \rangle\]

• Step 3

  $q_0$에 HAD를 통과시킵니다.

  \[\begin{aligned} q= &\frac{1}{\sqrt{2}}c_0 d_0 | 000 \rangle + \frac{1}{\sqrt{2}}c_0 d_0 | 100 \rangle + \\ &\frac{1}{\sqrt{2}}c_0 d_1 | 001 \rangle + \frac{1}{\sqrt{2}}c_0 d_1 | 101 \rangle + \\ &\frac{1}{\sqrt{2}}c_1 d_0 | 010 \rangle + \frac{1}{\sqrt{2}}c_1 d_0 | 110 \rangle + \\ &\frac{1}{\sqrt{2}}c_1 d_1 | 011 \rangle + \frac{1}{\sqrt{2}}c_1 d_1 | 111 \rangle \end{aligned}\]

• Step 4

  $q_0$가 $1$인 경우에 $q_1$과 $q_2$를 서로 SWAP해 주는 CSWAP을 통과시킵니다.

  \[\begin{aligned} q= &\frac{1}{\sqrt{2}}c_0 d_0 | 000 \rangle + \frac{1}{\sqrt{2}}d_0 c_0 | 100 \rangle + \\ &\frac{1}{\sqrt{2}}c_0 d_1 | 001 \rangle + \frac{1}{\sqrt{2}}d_0 c_1 | 101 \rangle + \\ &\frac{1}{\sqrt{2}}c_1 d_0 | 010 \rangle + \frac{1}{\sqrt{2}}d_1 c_0 | 110 \rangle + \\ &\frac{1}{\sqrt{2}}c_1 d_1 | 011 \rangle + \frac{1}{\sqrt{2}}d_1 c_1 | 111 \rangle \end{aligned}\]

• Step 5

  $q_0$에 HAD를 통과시킵니다.

  \[\begin{aligned} q= &\frac{1}{2}c_0 d_0 | 000 \rangle + \frac{1}{2}c_0 d_0 | 100 \rangle + \frac{1}{2}d_0 c_0 | 000 \rangle - \frac{1}{2}d_0 c_0 | 100 \rangle + \\ &\frac{1}{2}c_0 d_1 | 001 \rangle + \frac{1}{2}c_0 d_1 | 101 \rangle + \frac{1}{2}d_0 c_1 | 001 \rangle - \frac{1}{2}d_0 c_1 | 101 \rangle + \\ &\frac{1}{2}c_1 d_0 | 010 \rangle + \frac{1}{2}c_1 d_0 | 110 \rangle + \frac{1}{2}d_1 c_0 | 010 \rangle - \frac{1}{2}d_1 c_0 | 110 \rangle + \\ &\frac{1}{2}c_1 d_1 | 011 \rangle + \frac{1}{2}c_1 d_1 | 111 \rangle + \frac{1}{2}d_1 c_1 | 011 \rangle - \frac{1}{2}d_1 c_1 | 111 \rangle \\ = &c_0 d_0 | 000 \rangle + \frac{1}{2}(c_0 d_1 + c_1 d_0) | 001 \rangle + \\ &\frac{1}{2}(c_0 d_1 + c_1 d_0) | 010 \rangle + c_1 d_1 | 011 \rangle + \\ &\frac{1}{2}(c_0 d_1 - c_1 d_0) | 101 \rangle + \frac{1}{2}(-c_0 d_1 + c_1 d_0) | 110 \rangle \end{aligned}\]

  $q_1$과 $q_2$가 동일한 Qubit인 경우에는($c_0=d_0$, $c_1=d_1$) 다음과 같이 $q_0$를 읽었을 때 100%의 확률로 $0$로 읽히는 것을 확인할 수 있습니다.

  \[q=c_0^2 | 000 \rangle + c_0 c_1 | 001 \rangle + c_0 c_1 | 010 \rangle + c_1^2 | 011 \rangle\]

  $q_1$과 $q_2$가 다른 Qubit인 경우에는 $q_0$를 읽었을 때 $1$로 읽히는 경우가 있을 수 있습니다. 만약에 $c_0=1$, $c_1=0$, $d_0=0$, $d_1=1$라고 하면 다음과 같이 $q_0$를 읽었을 때 50%의 확률로 $0$이 읽히고 50%의 확률로 $1$이 읽히는 것을 확인할 수 있습니다.

  \[q=\frac{1}{2} | 001 \rangle + \frac{1}{2} | 010 \rangle + \frac{1}{2} | 101 \rangle - \frac{1}{2} | 110 \rangle\]

  $q_0$를 읽었을 때 항상 $0$이 읽히는지 아니면 가끔 $1$이 읽히는지를 보고 $q_1$과 $q_2$가 동일한 State를 가지고 있는 Qubit인지를 확인할 수 있습니다.

  앞의 CSWAP설명을 보면 위에서 첫 번째 Qubit은 그대로 출력한다고 하였습니다. 그런데 여기를 보면 위에서 첫 번째 Qubit이 그대로 출력되지 않은 것을 확인할 수 있습니다. 이것은 CSWAP을 쉽게 이해할 수 있도록 Superposition을 고려하지 않고 설명을 했기 때문입니다. 이처럼 Quantum Logic Gate는 Superposition을 사용할 때 전혀 직관적이지 않게 작동하는 경우가 많기 때문에 주의해야 합니다.

Conclusion

이 글에서는 Quantum Computer Program의 개발을 위해 필요한 기초지식을 소개하였습니다. 읽어보시고 느끼셨겠지만 여기서 얻은 정보만 가지고 Quantum Computer Program을 작성하기는 쉽지 않습니다. Computer Program으로 비유하면 AND, OR, NOT, XOR, NAND, NOR, XNOR의 Digital Logic Gate를 주고 복잡한 Program을 만들어야 되는 상황이라고 이해할 수 있습니다. 그리고 Quantum Logic Gate는 Digital Logic Gate처럼 직관적이지도 않아서 Quantum Logic Gate만 가지고 Program을 작성하기는 매우 어렵습니다. 하지만 다행스럽게도 현재 많은 기업들이 Quantum Computer Program의 개발을 위해 노력을 하고 있고, Quantum Computer를 Cloud환경에서 직접 사용해 볼 수 있는 환경이 갖추어지고 있으며, Quantum Computer용 Program을 작성하기 위한 전용 Programming Language가 개발되고 전용 Compiler가 개발되고 있는 등, 개발 환경이 점점 좋아지고 있는 관계로 가까운 미래에 쉽고 직관적으로 Quantum Computer Program의 작성이 가능해 질 것으로 기대합니다.