모나드와 함수형 아키텍처
모나드와 함수형 아키텍처
안녕하세요. 데이블에서 모바일 서비스를 개발하고 있는 김성철입니다. 이 글은 모나드와 함수형 프로그래밍을 이해하기 위해서 지난 1년여간을 생각하고 정리한 내용을 담은 것입니다. 총 5장으로 구성되어 있으며 6장에는 글의 흐름과 약간 관련 없는 내용을 추가로 담고 있습니다. 어떤 부분은 부족할 것이고 어떤 부분은 과장 되었을지도 모릅니다. 그러나 모나드에 관한 글을 꼭 한번 써보고 싶었습니다. 모나드를 생각하고 정리해오면서 저 자신도 많은 성장이 있었던 것 같습니다. 수정할 내용 또는 피드백이 있으시다면 sungcheol@dable.io 또는 skyfe79@gmail.com으로 보내주세요. 그래야 저도 더 성장할 수 있을 것 같습니다. :)
1장. 시작하기
모나드를 얘기하기 전에 몇 가지를 정리하려고 합니다.
1-1. 타입
타입. 우리가 코드를 작성할 때 늘 사용하는 그 타입이 맞습니다. string, int, float, double 등. 원시타입(Primitive type) 이외에도 enum, struct, class 등을 사용하여 우리가 원하는 타입을 추상화를 통해 만들 수 있습니다. 이 글에서는 이렇게 만들어진 타입을 집합으로 생각합니다.

네. 타입은 고등학교 수학에서 제일 처음에 나오는 그 집합입니다.
\[Boolean = \{ False, True \}\] \[Int = \{ ... -2, -1, 0, 1, 2, ... \}\] \[Double = \{ ... 0.9, 0.99, 0.999 ... 1.0 ... \}\] \[String = \{ "", "a", "aa", "aaa", ... "b" ... \}\]집합 원소 간에 연산할 때, 닫힘과 열림이라는 중요한 얘기가 나옵니다. 이에 대한 내용은 이 글 후반부인 닫힘과 열림에서 다루겠습니다. 지금은 타입은 집합이다.라고 생각합니다.
1-2. 함수
MS-DOS에서 터보 C를 사용하여 프로그래밍을 공부할 때, 함수는 명령어 집합 또는 작은 프로그램 단위라고 배웠습니다. 어떤 기능을 하는 코드들을 묶어 하나의 명령어처럼 사용할 수 있도록 함수를 정의했습니다. 함수를 이렇게 생각할 수 있지만, 이 내용은 수학에서 정의하는 함수와 거리가 멉니다. 하지만 함수형 프로그래밍에서 함수는 수학적 정의를 따르고 있습니다. 함수는 두 집합을 연결하여 관계를 만들어 주는 연산으로 정의합니다.
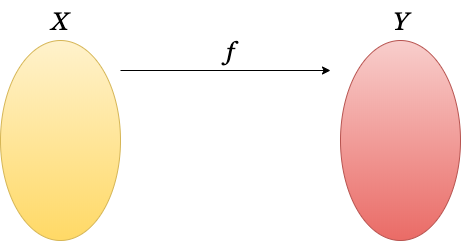
함수 $f$ 는 $X$와 $Y$를 연결하여 관계를 만들어 주는 함수입니다. 이러한 관계를 앞으로 $f: X \rightarrow Y $ 라고 표현하겠습니다. 이 관계에는 $ g: X \rightarrow X $ 도 있고 $ h: Y \rightarrow Y $ 도 있습니다. 우리가 매일 접하는 일상에서 예를 찾아보면, 웹사이트의 링크가 좋을 것 같습니다. 스마트폰에서 구글, 네이버 또는 다음과 같은 사이트에 접속하여 관심 있는 내용의 링크를 클릭하면 해당 내용을 다루는 사이트로 이동합니다. 링크를 사이트를 연결해주는 함수로 생각할 수 있습니다. 링크에는 같은 페이지 내에서 이동하는 Anchor 링크가 있고 다른 페이지로 이동하는 아웃 링크가 있습니다. 아웃 링크는 $f: X \rightarrow Y $ 라고 볼 수 있고 앵커 링크는 $ g: X \rightarrow X $ 또는 $ h: Y \rightarrow Y $ 라고 할 수 있습니다.
1-3. 합성
함수 $f$, $g$가 아래와 같을 때,
\[f: X \rightarrow Y\] \[g: Y \rightarrow Z\]두 함수를 합성한 합성 함수가 존재합니다.
\[g \circ f: X \rightarrow Z\]두 함수를 합성한 합성 함수가 존재합니다.

함수 합성은 정말 중요한 개념입니다. 함수를 합성할 수 있어야 확장이라는 개념을 만들 수 있기 때문입니다. 개인적으로도 함수 합성을 이해했을 때 그 설렘을 잊을 수 없습니다. 마치 빅뱅처럼 느껴졌기 때문입니다. 그리고 함수를 합성할 수 있어야 큰 문제를 작은 단위로 쪼개어 해결한 후 그 결과들을 모아 큰 문제를 해결할 수 있습니다.
인터넷을 생각해 봅시다. 인터넷이 폭발적으로 성장할 수 있었던 이유는 링크가 존재했기 때문입니다. 링크는 웹사이트 문서에서 다른 웹사이트 문서로 연결하는 방법입니다. 링크는 함수의 관계를 의미하며 링크를 계속 클릭하여 웹사이트를 계속 탐험하는 것은 함수 합성으로 이해할 수 있습니다.
우스갯소리로 수학자가 타임머신을 만드는 방법은 무엇일까요?
\[T: Present \rightarrow Future\]바로 현재에서 미래로 연결해 주는 함수를 찾으면 됩니다. 함수 $T$는 아래처럼 무수한 함수로 합성되어 있을 것입니다.
\[T: z \circ x \circ y \circ ... c \circ b \circ a\]그러나 함수 $T$ 를 찾거나 개발하는 일은 불가능하거나 몹시 어려운 일이 될 것입니다. 왜 그럴까요? 그것은 Side Effect(이하 사이드이펙트) 때문입니다.
수학에서 다루는 함수는 모두 Pure Function(이하 순수함수)입니다. 함수 $T$를 구성하는 모든 함수가 순수함수이어야 함을 의미합니다. 어떻게 하여 현재에서 미래로 한번 이동했다고 해도 항상 성공할 수 없다면 그 방법은 순수함수가 될 수 없습니다.
함수 $ f: X \rightarrow Y $ 에 집합 $X$의 원소를 함수 $f$에 대입하면 집합 $Y$의 원소가 나옵니다. 그리고 함수 $f$가 항상 이러한 성질을 유지할 때, 함수 $f$를 순수함수라고 부릅니다.
1-4. 사이드이펙트
순수함수는 동일한 인자가 주어졌을 때 항상 동일한 결과를 반환해야 하고 외부의 상태를 변경하지 않는 함수입니다. 외부 상태를 변경하지 않는다는 것은 외부에 있는 무엇을 변경하거나 의지하지 않는다는 것을 의미합니다. 순수함수는 외부상태에서 독립한 독립함수이어야 합니다. 함수 $f$가 외부 상태를 변경하지 않고 다른 함수 $g$가 외부상태를 변경했을 때, 함수 $f$에 같은 인자를 주었지만 다른 결과값을 반환하면 함수 $f$는 순수함수가 아닙니다. 외부환경 변화에 의해 변화를 받았기 때문입니다. 함수 $f$가 외부상태를 읽어 사용하여 자신이 만드는 결과에 영향을 준다면 외부 상태에 의존하고 있는 것입니다.
사이드이펙트는 어떤 함수가 존재할 때, 이 함수가 순수함수가 될 수 없게 만드는 모든 것을 의미합니다. 우리가 출근하거나 학교에 가는 길을 생각해 봅시다. 출근길이나 등굣길에 걸리는 시간을 교통수단의 합성으로 표현해 보겠습니다. 각 교통수단은 한 장소에서 다른 장소로 이동하는 함수입니다.
\[교통수단: 장소A \rightarrow 장소B\] \[출근시간: 도보 \circ 지하철 \circ 버스 \circ 도보\]우리는 매일 같은 방법으로 출근하고 등교하지만 출근 시간이나 등교 시간을 항상 일정하게 맞출 수가 없습니다. 다만 예측할 수 있을 뿐입니다. 그 이유는 도보 속도가 매일 다를 것이고 버스가 오는 시간도 매일 다를 것이고 지하철이 오는 시간도 매일 다를 것이기 때문입니다. 즉, 위 함수들이 순수함수가 아니기 때문에 그 합성으로 이루어진 출근 시간도 순수함수가 아닌 것이 됩니다. 사이드이펙트 때문입니다.
프로그래밍에서 말하는 사이드이펙트는 무엇이 있을까요? 함수가 반환해야 하는 결과를 반환하지 못하게 하는 모든 것을 의미합니다. 파일 이름을 주면 해당 이름을 갖는 파일 포인터를 반환하는 함수를 생각해 봅시다.
\[f: Name \rightarrow FILE\]파일 이름에 해당하는 파일이 없을 때는 FILE을 반환할 수 없습니다. 이번에는 네트워크 API 요청을 생각해 봅시다.
\[g: Request \rightarrow Response\]우리는 요청 $Request$를 보냈을 때 항상 응답 $Response$를 받을 수 없음을 잘 알고 있습니다. 서버 코드에 버그가 있을 수도 있고 통신이 안되는 음영지역에서 요청을 보낼 수도 있고 때로는 서버 머신을 호스팅하는 곳에 정전이 발생할 수도 있습니다. 이러한 점도 클라이언트와 서버에게는 사이드이펙트가 됩니다.
간단한 예로 객체지향 언어에서 발생하는 사이드이펙트를 살펴봅시다. 객체지향 언어는 class 내부에 멤버 함수와 멤버 변수를 정의할 수 있습니다. 멤버 함수는 this 포인터를 통해 멤버 변수를 사용하는 경우가 많습니다. 이 경우 this 포인터를 사용하는 것 자체가 외부환경에 의존하는 것입니다.
class SomeClass {
var factor: Int = 1
fun calc(value: Int): Int {
return value * this.factor
}
}
calc(value:) 함수에 동일한 인자가 주어졌을 때 동일한 결과값을 반환하는 것은 factor 멤버 변수가 어떻게 관리되는냐에 달려 있습니다. 위의 코드는 좋지 않은 코드입니다. 위와 같은 상황에서는 아래처럼 변경하는 것이 좋습니다.
class SomeClass {
private const val factor: Int = 1
fun calc(value: Int): Int {
return value * this.factor
}
}
즉, factor를 외부에서 접근할 수 없게 하고 상수로 정의하여 값이 수정될 가능성을 제거했습니다. 상수는 클래스의 모든 인스턴스에서 동일하므로 Kotlin에서 static 성격을 갖는 companion object의 멤버로 만들어주어야 합니다.(사실 Kotlin에서는 이러한 이유로 각 클래스마다 동일한 const val 을 가질 수 없습니다. 위 코드는 컴파일되지 않습니다.)
class SomeClass {
companion object {
private const val FACTOR: Int = 1
}
fun calc(value: Int): Int {
return value * FACTOR
}
}
만약 calc(value:)함수에 다른 factor를 적용해야 하면 factor를 인자로 받는 것이 좋습니다.
class SomeClass {
fun calc(value: Int, factor: Int): Int {
return value * factor
}
}
이렇게 하면 calc 함수를 사용하는 쪽에서 값과 factor 값을 주어 결과값을 예상할 수 있고 테스트할 수 있습니다. 그렇다면 사이드이펙트가 나쁜 것일까요? 사실 사이드이펙트는 좋고 나쁜 것이 아닙니다. 시간이 흐르면 자연스럽게 증가하는 엔트로피처럼 시간이 흐를수록 사이드이펙트는 증가합니다.
자연에서는 사이드이펙트가 당연하지만 정확한 계산 결과를 만들어야 하는 컴퓨터 프로그램에서는 가능한 줄여야 합니다. 사이드이펙트는 시간이 지남에 따라 증가하기 때문에 소프트웨어를 구현한 후에도 지속해서 관리해 주어야 합니다.
1-5. 정리
지금까지 배운 내용을 정리하면 아래와 같습니다.
- 타입은 집합이다.
- 함수는 집합과 집합을 연결하는 연산이다.
- 함수 합성으로 인해 확장이 가능하다.
- 사이드이펙트는 자연스러운 것이다.
- 그러나 정확한 결과를 만들어야 하는 컴퓨터 프로그램에서는 줄여야 한다.
2장. 프로그래밍 패러다임
컴퓨터 프로그래밍 패러다임은 크게 구조적 프로그래밍, 객체지향 프로그래밍 그리고 함수형 프로그래밍으로 나눌 수 있습니다. 놀라운 사실은 이 패러다임들이 오래전에 모두 만들어졌다는 것입니다. 개발자들에게는 구조적 프로그래밍, 객체지향 프로그래밍, 함수형 프로그래밍 순으로 인식되고 사용되어 온 것 같습니다. 그 이유는 소프트웨어의 크기와 컴퓨터의 성능 때문이라고 생각합니다. 각 패러다임에서 중요하게 생각했던 내용을 살펴보겠습니다.
2-1. 구조적 프로그래밍
구조적 프로그래밍이 주로 사용되던 시절은 컴퓨터 성능이 좋지 않았습니다. 그리고 통신의 속도도 빠르지 않았습니다. 통신 속도가 빠를수록 주고받는 데이터 또는 콘텐츠의 크기도 같이 커지기 마련입니다. 이 시절에는 주로 텍스트를 주고받았습니다. 즉, 프로그램은 작고 단순했습니다. 멀티태스킹이 없던 시절이었습니다. 구조적 프로그래밍으로 구현하는 프로그램을 한마디로 표현하면 아래와 같습니다.
\[프로그램 = 데이터 + 로직\]구조적 프로그래밍의 시작은 다익스트라의 증명으로 시작되었습니다. 다익스트라는 순차, 분기, 반복만으로 모든 프로그램을 만들 수 있음을 증명했습니다. 순차는 프로그래밍 문(statement)이 순서대로 실행됨을 의미합니다. 분기는 if, then, else를 통한 로직 흐름의 방향 제어를 의미합니다. 반복은 do, while, for 등으로 순차와 분기를 반복할 수 있음을 의미합니다.
이 증명이 의미하는 것은 큰 문제를 작은 문제로 나누어 풀 수 있다.입니다.
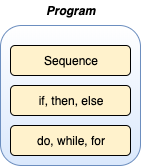
이 프로그램을 아주 가까이에서 들여다보면 아래처럼 여러 개의 작은 프로그램 또는 모듈로 구성되어 있을 것입니다.

작은 프로그램 또는 모듈도 순차, 분기, 반복으로 구성됩니다. 작은 프로그램 또는 모듈도 아주 가까이에서 들여다보면 또다시 작은 프로그램 또는 모듈로 나누어집니다. 재귀적으로 계속 들여다보면 결국 더는 쪼갤 수 없는 단위인 순차, 분기, 반복만이 남게 됩니다.
분할 정복 및 다이나믹 프로그래밍은 큰 문제를 작은 문제로 나누어 해결하는 방법입니다. 다익스트라의 증명에서부터 시작되는 것입니다. 이 증명으로 인해 우리는 함수를 작성할 때 최소 단위로 작성할 수 있게 되었고 최소단위로 구현된 함수들을 모아 규모가 큰 문제를 해결할 수 있는 것입니다.
2-2. 객체지향 프로그래밍
객체지향 프로그래밍은 1960년 발표된 시뮬라 67로부터 시작되었지만, 산업계와 개발자들에게 중요하기 인식되기 시작한 때는 1990년대 입니다. 컴퓨터 성능이 좋아지고 GUI가 등장하고 통신 속도가 빨라졌습니다. 인터넷이 보급 되기 시작하고 PC가 대중화 되면서 컴퓨터는 비즈니스만이 아닌 엔터테인먼트를 위한 장치가 되었습니다. 텍스트와 함께 이미지를 포함한 다양한 멀티미디어 콘텐츠를 소비했습니다. 혼자하는 가정용 게임에서 벗어나 함께 하는 온라인 게임으로 점점 이동했습니다. IT산업의 규모가 커지게 되었고 IT기술로 풀어야할 다양한 문제들이 출현하면서 문제의 복잡도가 증가했습니다.
객체지향 프로그래밍을 대표하는 클래스는 로직과 데이터를 담아 아주 작은 모듈을 만들 수 있는 좋은 방법입니다. 그리고 컴퓨터 성능이 좋아지면서 실행시간에 실행할 메서드를 결정하는 동적 바인딩이 문제가 되지 않았습니다. 사람들은 클래스를 잘 활용하면 레고 블록을 조립하듯 프로그램을 개발할 수 있다고 생각했습니다. 레고 블록을 쉽게 교체할 수 있듯이 변경에 쉽게 대처할 수 있어 유지보수에도 탁월하다고 생각했습니다. 객체지향 프로그래밍으로 구현하는 프로그램을 한마디로 표현하면 아래와 같습니다.
\[클래스 = 데이터 + 로직\] \[프로그램 = 클래스 + 관계\]데이터와 로직은 클래스라는 커스텀 타입으로 포장되었습니다. 여러 클래스가 서로 관계를 맺으며 문제를 해결하고 프로그램을 구성합니다. 관계는 클래스들이 서로 메시지를 주고받으며 형성합니다.
객체지향 프로그래밍은 프로그램을 모듈화하여 개발하는데 아주 좋은 방법입니다. 하지만 프로그램의 규모가 커지면 문제의 복잡도도 동시에 증가합니다. 레고 블록처럼 프로그램을 개발할 수는 있었지만, 유지보수가 쉬워진 것은 아니었습니다. 그 이유는 클래스를 강한 응집력과 약한 결합력을 갖추어 설계하는 게 어려웠기 때문입니다. 이렇게 설계하는 것은 객체지향에 대한 많은 경험을 요구합니다. 그리고 클래스도 타입이고 관계도 클래스 간의 메시지를 주고받으며 형성되는 로직으로 볼 수 있기 때문에 프로그램 = 데이터 + 로직이었던 구조적 프로그래밍과 크게 다르지 않습니다. 문제와 복잡도도 증가하면서 유지보수도 어려워졌습니다. 유지보수가 어려운 이유는 여러 가지가 있습니다. 디펜던시도 큰 이유지만 사이드이펙트도 중요한 이유 중 하나입니다. 프로그램 규모가 커지면서 협업을 통한 개발이 일반화되었습니다. 그러면서 사이드이펙트가 커지게 되었죠. 클래스를 만들 때 사이드이펙트를 최대한 줄이고 적절한 테스트를 작성해야 합니다. 그래야 원치 않는 사이드이펙트가 발생한 시점을 알고 대처할 수 있습니다.
2-3. 함수형 프로그래밍
함수형 프로그래밍이 주요하게 인식된 것은 근래입니다. 요즘은 1080p를 넘어 4K동영상을 온라인 콘텐츠로 소비하는 시대입니다. PC뿐 아니라 모바일도 싱글 코어가 아닌 멀티 코어가 일반화 되었으며 GPU도 일반화 되었습니다. 동시성뿐만 아니라 병렬성도 대두되었습니다. 개발자가 작성하는 for 루프는 싱글 코어용 코드이지만 프로그래밍 언어가 자체 담고 있는 forEach는 멀티 코어용으로 최적화된 코드입니다. 개발자가 직접 최적화된 for 루프를 만들 필요가 사라졌습니다. 있는 forEach를 그저 사용하기만 하면 됩니다. 마치 HTML의 태그처럼 이미 있는 것을 선언하여 사용하면 그만인 시대가 되었습니다.
수학적 함수와 구조적 프로그래밍에서 사용되는 함수에는 차이가 있습니다. 함수형 프로그래밍은 수학적 함수를 따릅니다. 그리고 구조적 프로그래밍과 객체지향 프로그래밍은 구조적 프로그래밍에서 사용되는 함수를 따릅니다. 그렇다면 둘의 차이가 무엇일까요? 바로 사이드이펙트입니다. 수학적 함수는 순수함수입니다. 순수함수는 사이드이펙트가 없는 함수입니다. 오로지 인자값에만 의존하여 결과값을 만듭니다. 구조적 프로그래밍의 함수는 프로그램의 상태를 변경할 수 있습니다. 글로벌 변수를 변경하기도 하고 객체지향 프로그래밍의 멤버 함수는 this 포인터를 사용하여 멤버 변수의 값을 변경하기도 합니다.
순수 함수는 사이드이펙트가 없어서 함수를 실행해도 외부에 영향을 주지 않아 독립적입니다. 그래서 스레드에 안전하고 병렬로 실행할 수 있습니다. 하지만 구조적 프로그래밍과 객체지향 프로그래밍에서는 함수와 공유 자원의 스레드 안전성은 항상 중요한 주제였습니다.
함수형 프로그래밍이 요즘 와서 대두되는 이유는 함수형 프로그래밍에서 중요한 주제인 불변성(immutable)을 지키기 위해서 많은 메모리와 높은 컴퓨터 성능이 필요하기 때문입니다. 불변성을 지키는 가장 쉬운 방법은 모든 값을 복사하는 것입니다. 예를 들어, 다음 코드를 살펴봅시다.
let numberList = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
numberList
.filter { $0 > 5 }
.map { $0 * 10 }
.forEach { print($0) }
코드를 실행하면 numberList는 filter에 복사되어 전달됩니다. 만약 복사되지 않고 참조나 포인터로 numberList가 전달된다면 filter함수는 외부에 있는 numberList에 의존하는 것이므로 filter 함수는 더 이상 순수 함수가 아닌 것이 됩니다. map 함수에 전달되는 인자도 filter 함수를 통해 나온 결과값이 복사된 것입니다. forEach 함수에 전달되는 인자도 map 함수의 결과값이 복사된 것입니다.
컴파일러 최적화 및 언어 구현 최적화 등을 논외로 할 때, 아주 많은 원소를 가진 리스트를 매번 복사한다면 어떨까요? 많은 메모리와 높은 성능을 갖춘 컴퓨터가 필요할 것입니다. 물론 실제로 이렇게 작동하지는 않습니다. 목록을 한 번에 모두 복사하는 것이 아니라 한 번에 원소 하나씩 복사하면 어떨까요? 원소 1로 $filter \rightarrow map \rightarrow forEach$를 수행하고 다음 원소 2에 같은 작업을 수행합니다. 이렇게 할 때 좋은 점은 멀티 코어를 활용할 수 있다는 것입니다. 만약 10개의 코어를 가진 CPU라면 코어마다 원소 한 개씩 실행하여 최적화를 할 수 있을 것입니다.
순수 함수형 프로그래밍을 지원하는 헤스켈을 제외하면 Kotlin, Swift와 같은 언어들은 모두 멀티 패러다임 언어입니다. 즉, 구조적, 객체지향 그리고 함수형 프로그래밍을 모두 지원합니다. 거인의 어깨 위에 올라앉듯 구조적 또는 객체지향 프로그래밍으로 만들어진 수많은 라이브러리와 프레임워크를 바탕으로 함수형 프로그래밍을 도입하는 것이 좋을 것 같습니다. 함수형 프로그래밍이 대두되면서 개발자들 사이에서 mutable과 immutable 그리고 사이드이펙트가 자주 얘기되는 것 같습니다. 함수형 프로그래밍을 사용하지 않아도 작성하는 함수나 타입이 되도록 불변성을 지키고 사이드이펙트를 낮추는 방향으로 개발하는 것 같습니다.
객체지향 프로그래밍에서 만든 클래스도 타입입니다. 그리고 함수형 프로그래밍에서 함수는 일급 객체로 타입 집합에 속한다고 볼 수 있습니다. 타입은 변수로 선언할 수 있습니다.
var number: Int = 10
변수가 된다는 것은 어떤 의미를 가질까요? 함수의 인자로 전달될 수 있고 함수의 결과로 반환될 수도 있습니다. 사람의 몸에 피가 흐르듯 변수는 프로그램의 로직을 흐를 수 있습니다. 그러다가 값이 필요하면 변수에서 값을 읽고 새로운 값을 기록해야 하면 변수에 새로운 값을 기록합니다.
함수가 일급 객체라는 의미는 변수에 함수를 담을 수 있다는 것입니다. 그리고 함수의 인자로 전달되고 함수의 결과로 반환될 수 있음을 의미합니다.
typealias Converter = (Int) -> Int
val triple: Converter = {
it * 3
}
인자로 전달한 값을 3배 증가시키는 함수를 triple이라는 변수에 담았습니다. triple은 변수이기 때문에 프로그램의 로직을 흐를 수 있습니다. 그러다가 값이 필요하면 변수에서 값을 읽듯이 triple에 담긴 함수를 실행하여 값을 얻을 수 있습니다. 즉, 기존에는 값만이 변수에 담겨 흐를 수 있었지만, 함수형 프로그래밍에서는 로직이 변수에 담겨 흐를 수 있는 것입니다. 함수형 프로그래밍은 람다를 사용하여 함수를 일급 객체로 만듭니다. 물론 C언어에서 함수 포인터를 사용해서 같은 효과를 만들 수 있습니다.
#include <stdio.h>
typedef int (*const Converter)(int);
int someConverter(int number) {
return number * 3;
}
int main() {
Converter triple = someConverter;
printf("%d\n", triple(10));
return 0;
}
하지만 람다와 함수 포인터는 큰 차이가 있습니다. 바로 제네릭 지원과 실행을 지연할 수 있다는 점입니다. 람다는 값이 실제로 필요할 때까지 실행을 지연할 수 있습니다. 그리고 제네릭을 아주 쉽게 지원합니다. 그러나 C언어에서 이를 구현하기 위해서는 큰 노력이 필요합니다.
typealias Converter<T> = (T) -> T
fun <T> convert(value: T, converter: Converter<T>): T {
return converter(value)
}
fun main(args: Array<String>) {
val input = Scanner(System.`in`)
val value = input.nextDouble()
println(convert(value) { it * 10})
}
다른 예를 살펴봅시다. 제네릭 함수로 2개의 인자를 더하는 함수를 만들어 봅시다.
fun <T> add(a: T, b: T): T {
return a + b
}
이 함수는 컴파일이 될까요? 컴파일이 되지 않습니다. 제네릭은 타입을 지우는 것이어서 타입 T가 + 연산자를 지원하는지 안 하는지 알 수 없습니다. 이럴 경우 연산 부분에 람다를 적용하면 아주 쉽게 문제를 해결할 수 있습니다. 람다를 구현할 때는 제네릭 타입 T가 구체화되어 있기 때문입니다.
fun <T> add(a: T, b: T, op: (T, T) -> T): T {
return op(a, b)
}
val result = add(10, 20) { a, b -> a + b }
주의할 점은 연산 부분에 람다를 적용한 것입니다. 제네릭 타입을 사용하여 지워진 연산자 내용을 개발자가 람다로 채우는 것입니다. 아래 같은 경우에는 람다를 사용하여도 제네릭과 동일한 문제가 발생합니다. 이럴 경우, 제네릭 타입 T에 타입 제약 등을 적용해 + 연산이 가능함을 컴파일러에 알려줘야 합니다.
fun <T> add(a: T): (T) -> T {
return { b ->
a + b
}
}
실행지연을 사용하면, 커링을 적용하여 다양한 연산자를 만들 수 있습니다. 두 수를 더하는 함수는 보통 아래와 같을 것입니다.
fun add(a: Int, b: Int): Int {
return a + b
}
커링을 적용하면 아래와 같이 만들 수 있습니다.
fun add(a: Int): (Int) -> Int {
return { b ->
a + b
}
}
위 add 커링 함수를 사용하여 연산자를 만들어 보겠습니다.
val op10plus = add(10)
그리고 아래와 같이 특정 상황에서 op10plus를 실행하여 원하는 결과를 얻을 수 있습니다.
fun main(args: Array<String>) {
val op10plus = add(10) { a, b -> a + b}
val numberList = listOf(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
val result = numberList.map { op10plus(it) }
println(result)
}
커링 함수에 제네릭을 적용하여 연산자를 만들 수도 있습니다.
fun <T> operator(a: T, op: (T, T) -> T): (T) -> T {
return { b ->
op(a, b)
}
}
fun main(args: Array<String>) {
val op10plus = operator(10) { a, b -> a + b}
val numberList = listOf(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
val result = numberList.map { op10plus(it) }
println(result)
}
변수 op10plus에 로직을 담아 필요할 때까지 실행을 지연시키고 numberList.map 함수에서 값을 생성하기 위해 사용되었습니다. 람다의 얘기가 좀 길어졌습니다. 람다 이외에도 함수형 프로그래밍의 함수는 수학적 순수 함수를 따른다라는 내용이 너무나 중요합니다. 모나드를 이해하는 핵심 열쇠이기 때문입니다. 함수형 프로그래밍으로 작성하는 프로그램을 한마디로 표현하면 아래와 같습니다.
타입에 대해서는 많은 얘기를 했지만 흐름에 관해서는 얘기하지 않았습니다. 3부에서 모나드를 알아보면서 ‘흐름’에 대해서 알아봅시다. 지금까지 컴퓨터 프로그래밍 패러다임을 간략하게 살펴보았습니다. 좀 더 자세하고 재미있는 얘기는 클린 아키텍처 - 소프트웨어 구조와 설계의 원칙, 로버트 C.마틴 지음 책에서 읽어보시길 권합니다.
3장. 모나드
\[a \circ b \circ c \circ ... \circ x \circ y \circ z\]함수 합성식입니다. 모나드뿐 아니라 함수형 프로그래밍의 본질이 모두 담겨 있는 식입니다. 사실 모든 이야기는 여기서부터 시작됩니다. 수학에서 이렇게 함수를 합성할 수 있는 이유는 수학의 함수가 순수 함수이기 때문입니다. 1부. 시작하기에서 함수는 두 집합을 연결하여 관계를 만들어 주는 연산으로 정의했습니다. 두 집합을 연결할 때 닫힘과 열림이라는 중요한 얘기를 해야 합니다.
3-1. 닫힘과 열림
집합 $A$에 대하여 이항연산을 수행할 때 연산 결과가 같은 집합 $A$의 원소이면 해당 이항연산은 집합 $A$에 닫혀 있다고 합니다. 자연수 집합 $N$에서 $+$연산은 자연수 집합에 닫혀 있습니다.
\[1 + 2 = 3\]집합 $A$에 대하여 이항연산을 수행할 때 연산 결과가 같은 집합 $A$의 원소가 아니면 해당 이항연산은 집합 $A$에 열려 있다고 합니다. 자연수 집합 $N$에서 $-$연산은 자연수 집합에 열려 있습니다.
\[1 - 1 = 0\]$0$은 자연수 집합에 포함되어 있지 않기 때문에 자연수 집합 $N$에서 $-$ 연산은 열려 있습니다. 열려 있는 경우에는 우리가 알고 있는 집합이 확장되는 것으로 볼 수 있습니다. 연산 결과로 연결되어야 할 집합을 찾게 된 것입니다. 이 예제에서 우리는 $0$을 포함하고 있는 정수 집합 $Z$를 찾게 된 것입니다. 한 번 더 예를 들어보겠습니다. 정수 집합 $Z$에 $\times$ 연산은 열려 있습니다.
\[-1 \times -2 = 2\]하지만 $\div$ 연산은 열려 있습니다.
\[1 \div 10 = 0.1\]정수 집합은 나눗셈 연산에 열려 있으며 0.1이 포함된 새로운 집합을 찾아야 합니다. 유리수 집합 $Q$를 찾게 됩니다. 이제 우리가 알고 있는 수의 집합은 자연수에서 유리수까지 확장되었습니다. 이를 정리하면 아래와 같습니다.
\[A: N \rightarrow N\] \[f: N \rightarrow Z\] \[B: Z \rightarrow Z\] \[g: Z \rightarrow Q\] \[C: Q \rightarrow Q\]위 정리에서 $f$는 $-$ 연산에 해당하고 $g$는 $\div$ 연산에 해당합니다. 이것을 보고 사람들은 $f$와 $g$를 합성할 수 있지 않을까? 생각했습니다.
\[g \circ f: N \rightarrow Q\]이를 그림으로 표현하면 아래와 같습니다.

이 그림은 카테고리 이론(이하 범주론)을 설명하는 그림입니다. 그림에서 $A$, $B$, $C$ 를 연결하는 화살표에서 $f: A \rightarrow B$ 가 있고 $g: B \rightarrow C$ 가 존재하면 반드시 $g \circ f: A \rightarrow C$ 가 존재한다는 것이 카테고리 이론입니다. 카테고리 이론은 수학의 여러 분야에서 공통으로 발생하는 현상들을 추상화를 통해 정리한 분야입니다. 함수 합성을 중심으로 추상화를 합니다. 카테고리 이론으로 컴퓨터 프로그램을 추상화하면 함수의 합성으로 추상화할 수 있습니다. 컴퓨터 프로그램의 모든 것을 함수의 합성으로 표현하기 위해서 카테고리, 펑터, 모노이드, 모나드 등을 사용합니다.
카테고리 이론에서 $g \circ f: A \rightarrow C$ 가 중요한 내용입니다. 이 정리가 있어서 함수 합성은 빅뱅처럼 폭발적으로 확장됩니다. 시간이 지날수록 컴퓨터 프로그램에 신규 기능을 추가하면 프로그램의 덩치가 커지는데 함수 합성을 적용하면 큰 문제 없이 확장할 수 있습니다.
\[p: g \circ f\] \[k: q \circ p\] \[...\]거꾸로 생각하면 덩치가 큰 문제를 작은 문제로 나누어 풀 수 있다는 것을 의미합니다. 텍스트 파일을 열어 모든 문자를 대문자로 변경한 후 화면에 출력하는 문제를 생각해 봅시다. 이 문제를 함수로 잘게 나누어 표현해 보면 아래와 같습니다.
\[p: 텍스트 파일 \rightarrow 텍스트 문자열\] \[q: 텍스트 문자열 \rightarrow 대문자 텍스트 문자열\] \[r: 대문자 텍스트 문자열 \rightarrow 대문자 텍스트 문자열 화면에 출력\]이 것을 카테고리 이론으로 표현해 보면 아래와 같습니다.
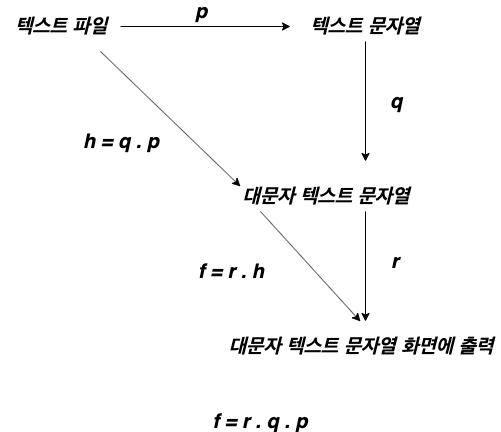
위처럼 작동하는 함수를 잘게 나누어 해결하고 각 결과를 합성하여 결국 원하는 함수를 만들 수 있음을 알 수 있습니다.
\[f: r \circ q \circ p\]카테고리 이론에 대한 정말 좋은 책이 있습니다. Category Theory for Programmers 책으로 온라인으로 무료로 제공되고 있습니다. 카테고리 이론에 관한 내용은 이 책을 참고하시면 좋을 것 같습니다.
3-2. 순수 함수와 사이드 이펙트
1부에서 사이드이펙트를 알아보았습니다. 사이드이펙트가 발생하는 위치에 따라 나누어 보면, 함수 외부와 내부에서 발생하는 사이드이펙트로 나눌 수 있습니다. 만약 독립된 함수로 외부에 영향을 주지도 받지도 않는 함수가 존재한다고 생각해 봅시다. 이 함수는 파일 이름을 받아 파일을 반환해야 하는 함수라면 어떨까요?
\[f: FileName \rightarrow FILE\]내부에서도 사이드이펙트가 발생하지 않고 항상 $FILE$을 반환한다면 함수 $f$는 순수함수가 될 것입니다. 하지만 $FileName$해당하는 파일이 없을 수도 있습니다. 이럴 때는 무엇을 반환해야 할까요? 포인터를 자주 사용하는 C언어에서는 이중 포인터를 사용하여 오류 발생 시 결과 이외의 오류 값을 담을 수 있는 Error 변수의 이중포인터를 함수 인자로 같이 넘겨 주곤 했습니다. C++, Java 같은 언어는 Exception을 도입하여 결과 이외의 값을 예외로 처리하도록 했습니다. 두 방법 모두 순수함수 성질을 깨는 것입니다. 순수 함수성이 깨지는 것을 조심해야 하는 이유는 함수 합성을 더 이상 할 수 없기 때문입니다. 즉, 독립된 함수일 때 결과값 집합 이외의 집합값을 반환할 때 사이드이펙트가 있다고 얘기할 수 있습니다.
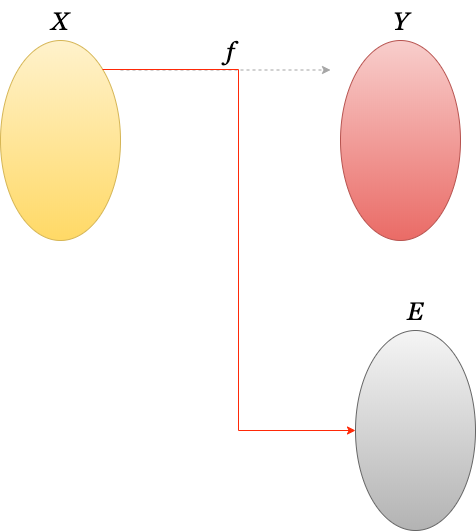
3-3. 모나드란 무엇인가?
그렇다면 이렇게 생각해 볼 수 있습니다. 결과값 집합과 오류값 집합을 하나의 집합으로 만들면 어떨까? 라고 말입니다.
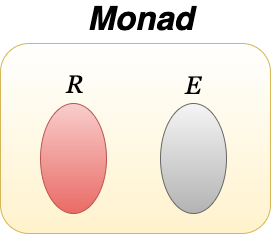
지금까지 말하고 싶었던 모나드는 함수 내부에서 발생할 수 있는 사이드이펙트를 결과 집합과 함께 포함하는 타입입니다. 함수 실행 결과를 항상 모나드로 반환하여 순수함수 성질을 잃지 않게 하는 것입니다. 더 정확하게 얘기하자면 원시타입(boolean, int, string, float, double)과 커스텀 타입(class, struct)을 구체타입이라고 할 때 우리는 구체타입을 사용하여 함수의 인자와 결과값을 표현했습니다. 이 구체타입을 한 번 더 추상화한 것이 모나드입니다.
\[f: FileName \rightarrow Monad[FILE, Error]\]노트 이후로 { 원시타입, enum, struct, class } 를 모나드와 비교해 구체타입으로 칭하겠습니다.
함수의 결과값에 모나드를 적용하면 내부에서 어떤 사이드이펙트가 발생하던 그 함수 자체는 순수 함수로 만들 수 있습니다. 이를 좀 더 응용하면 사이드이펙트가 아닌 다른 집합을 포함하는 타입을 생각할 수 있습니다. 자주 쓰는 모나드 중 $Either$가 대표적인 예입니다. $Either$모나드는 $Left$와 $Right$를 가지고 있는 타입으로 $Either[Left, Right]$라고 정의할 수 있습니다. $Either$에 대한 내용은 잠시 뒤에 다시 살펴보겠습니다.
모나드는 함수에 들어가고 반환되는 값을 한차례 추상화한 것입니다. $f: int \rightarrow int$ 함수가 있을 때, 함수 인자 또는 반환값을 추상화하는 것이죠. C++나 Java를 배울 때, 원시타입인 int, string, double, boolean 등을 모아 class를 통해 추상화하듯이 말이죠. 추상화는 한번 감싸는 것으로 생각할 수 있습니다. 그 과정에서 개발자는 어떤 의미를 심을 수 있습니다. C++에서 원시타입과 메서드를 모아 Person으로 추상화하듯이 말입니다. Maybe 모나드는 값이 있거나 없거나라는 의미를 담습니다. 이것이 모나드의 강력한 힘입니다. 구체타입을 추상화하면서 의미를 동시에 담을 수 있게 되어 마치 사람이 생각하는 것처럼 함수를 작성할 수 있습니다.
함수의 사이드이펙트를 포함하여 함수의 인자나 결과값을 추상화하는 모나드를 살펴보았습니다. 하지만 이것은 구조체나 클래스로도 정의 가능합니다. 하지만 모나드를 더욱 구분지어주는 특징이 하나 더 있습니다. 바로 합성을 통해 흐름을 만드는 것입니다. 흐름을 만들기 위해서 특별히 해주는 일이 있습니다. 어떤 것인지 살펴봅시다.
3-4. 합성, 흐름 그리고 빅뱅
우리는 거인의 어깨 위에 앉아 있습니다. 구조적 프로그래밍 그리고 객제지향 프로그래밍이 쌓아온 수많은 함수와 타입 위에 앉아 있는 것이지요. 모나드를 통해 함수를 합성하기 위해서는 함수의 인자와 결과값이 모두 모나드로 되어 있어야 합니다.
\[f: Monad \rightarrow Monad\] \[g: Monad \rightarrow Monad\] \[h: Monad \rightarrow Monad\] \[h \circ g \circ f: Monad \rightarrow Monad \rightarrow Monad\]간단한 Monad를 정의해 보겠습니다. Result<T>이란 모나드로 [Success, Fail] 집합을 포함합니다. 함수에서 내부 연산 중 사이드이펙트가 발생하면 Fail을 반환합니다.
sealed class Result<T> {
data class Success<T>(val value: T): Result<T>()
class Fail<T>: Result<T>()
}
Result
구체타입만을 쓰는 함수는 아래와 같을 것입니다.
fun div(a: Int, b: Int): Int {
return a / b
}
여러분도 잘 알듯이 이 함수는 사이드이펙트를 가지고 있습니다. 만약 b가 0일 경우 java.lang.ArithmeticException: / by zero라는 예외가 발생합니다. 이 예외를 처리해 보겠습니다.
fun div(a: Int, b: Int): Int {
try {
return a / b
} catch (e: Throwable){
return -1
}
}
만약 위처럼 작성했다면 문제는 해결할 수 있지만 결과값이 모호해집니다. div(a, -a) 또는 div(-a, a) 때의 결과값과 예외가 발생했을 때 반환하는 -1을 구분할 수 없기 때문입니다.
이제 결과값을 모나드로 추상화해 보겠습니다. 위에서 정의한 Result
fun div(a: Int, b: Int): Result<Int> {
try {
return Result.Success(a / b)
} catch (e: Throwable){
return Result.Fail()
}
}
실제로 사용해 봅시다.
val result1 = div(10, 2)
val result2 = div(10, 0)
위 result를 사용하려면 어떻게 해야 할까요? 각 result가 Success인지 Fail인지 검사해야 합니다. 아래처럼 말입니다.
fun main(args: Array<String>) {
val result1 = div(10, 2)
val result2 = div(10, 0)
when (result1) {
is Result.Success -> { println(result1.value) }
is Result.Fail -> { println("result1 is Failed") }
}
when (result2) {
is Result.Success -> { println(result2.value) }
is Result.Fail -> { println("result2 is Failed") }
}
}
아래는 출력된 결과입니다.
5
result2 is Failed
모나드 Result
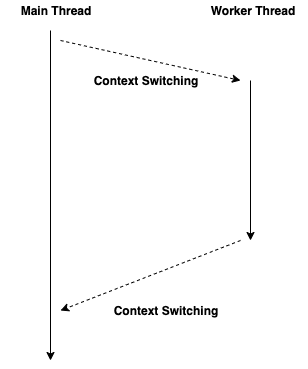
위 그림에서 워커 스레드에서 메인 스레드에 값을 바로 쓰거나 UI에 접근하거나 하면 프로그램이 오작동을 일으킬 수 있습니다. 그래서 콜백, Rx, async/await 등 그 어떤 것을 사용하더라도 컨텍스트 스위칭을 피할 수는 없습니다. 즉, 워커 스레드에서 계산한 값을 메인 스레드에서 사용하기 위해서는 어떤 번거로운 작업이 필요합니다.
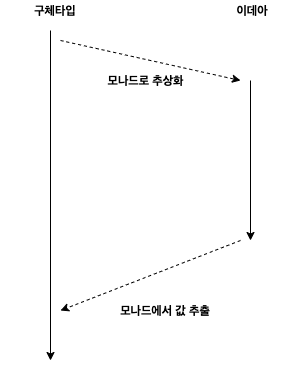
모나드를 사용한 코드가 이와 비슷하지 않나요? 마치 플라톤의 이데아 이론 같기도 합니다. 구체타입 세계와 추상화로 이뤄진 이데아가 있다고 볼 수 있습니다. 객체지향에서는 원시타입들을 class라는 도구를 사용해 추상화하였고 그것을 원시타입 세계에서 사용하기 위해서는 인스턴스를 만들어야만 했습니다. 모나드도 마찬가지입니다.
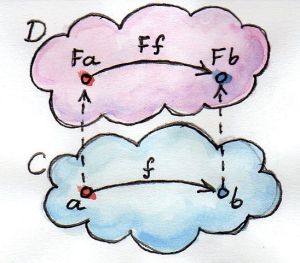
아래는 Category Theory for Programmers 책에서 Functor를 표현한 그림으로 구체타입 세계와 모나드 세계를 표현하고 있습니다.
기억할 점은 구체타입을 추상화한 모나드에서 값을 얻기 위해서는 스레딩의 컨텍스트 스위칭처럼 부가적인 작업이 필요하다는 것입니다.
위에서 만든 모나드를 통해서 함수를 합성해 봅시다. 어떤 정수를 입력하면 정수값에 10을 계속해서 곱하는 함수 합성입니다. 단, 0 이하의 값을 입력하면 Fail을 반환하고 모나드에서 값을 추출할 때 Fail이면 -1을 반환한다고 가정합니다.
fun a(value: Int): Result<Int> {
if (value > 0) {
return Result.Success(value * 10)
} else {
return Result.Fail()
}
}
fun b(value: Result<Int>): Result<Int> {
return when (value) {
is Result.Success -> {
Result.Success(value = value.value * 10)
}
is Result.Fail -> {
value
}
}
}
fun c(value: Result<Int>): Int {
return when (value) {
is Result.Success -> {
value.value
}
is Result.Fail -> {
-1
}
}
}
fun d(value: Int): Int {
return value * 10
}
위 함수 합성식을 코드로 나타내면 아래와 같습니다.
val result = c(b(b(b(b((a(10)))))))
println(result)
// 출력
1000000
val result = c(b(b(b(b((a(-10)))))))
println(result)
// 출력
-1
원하는 만큼 함수를 합성할 수 있습니다. 하지만 함수 합성식이 자연스럽지 않습니다. 코드를 이해하기가 더 어려워진 것 같습니다. 뭔가 흐르는 것처럼 표현할 수 있을까요? 멤버 함수나 연산자 재정의를 사용해 봅시다.
infix fun <T> Result<T>.compose(functor: (value: Result<T>) -> Result<T>): Result<T> {
return functor(this)
}
infix fun <T> Result<T>.compose2(functor: (value: Result<T>) -> T): T {
return functor(this)
}
functor 라는 람다를 받아서 functor를 실행하여 Result
위의 compose 함수를 사용하면 아래처럼 함수 합성식을 표현할 수 있습니다.
val result1 = a(10) compose ::b compose ::b compose ::b compose ::b compose2 ::c
println(result1)
// 출력
1000000
val result2 = a(-10) compose ::b compose ::b compose ::b compose ::b compose2 ::c
println(result2)
// 출력
-1
뭔가가 함수 사이로 흐르는 것 같습니다. compose 연산자를 사용하면 함수 a, b, c를 끝이 없이 합성할 수 있을까요? 그렇지 않습니다. 함수 a는 구체타입 T를 받아서 모나드 Result
val result3 = a(10) compose ::b compose2 ::c compose ::a // <- 여기서 연결이 끊어집니다.
만약 이를 해결하기 위해서 아래처럼 compose3를 정의한다고 생각해 봅시다.
infix fun <T> Result<T>.compose2(functor: (value: T) -> Result<T>): Result<T> {
when (this) {
is Result.Success -> {
functor(this.value)
}
is Result.Fail -> {
functor(어떤 값을 넣어야 하죠?)
}
}
}
네 그렇습니다. this는 현재 이데아를 걷고 있는 추상화된 모나드이기 때문에 functor에 구체타입 값을 넣어주기 위해서는 자기 자신으로부터 값을 추출해야 합니다. 하지만 위의 경우 어떤 값을 넣어야 할지 기준이 없습니다. 물론 첫 가정에서 Fail 때는 -1 을 반환하면 된다고 했지만, 그 가정이 변경되거나 정해지지 않았다면 어떤 값을 넣어야 할지 정할 수가 없습니다.
그리고 우리가 정의한 함수 a, b, c의 프로토타입을 살펴봅시다.
fun a(value: Int): Result<Int>
fun b(value: Result<Int>): Result<Int>
fun c(value: Result<Int>): Int
어떤가요? 우리는 보통 이런 식으로 함수를 정의하지 않습니다. 우리가 사용하는 외부 함수나 라이브러리 그리고 프레임워크의 함수들도 위처럼 정의되어 있지 않습니다. 구체타입을 인자로 받고 결과값을 반환합니다. 아래처럼 말입니다.
fun d(value: Int): Int
우리는 거인의 어깨 위에 앉아 있고 거인을 조종할 수 있어야 합니다. 즉, 거대한 라이브러리와 프레임워크의 함수들을 합성을 통해 사용할 수 있어야 합니다. 이 함수들을 감싸 안을 방법이 필요합니다.
3-5. map과 flatMap
위에서 정의한 Result
map 함수는 구체타입을 이데아로 연결해 주는 함수이며 flatMap 은 이데아를 계속 거닐게 해주는 함수입니다. flatMap의 이름에 flat이 들어가는 이유는 함수를 합성하다 보면 중첩된 Monad[Monad[V]]가 발생할 수 있기 때문에 이것을 펼쳐서 하나의 Monad[V]로 만들어 준다고 하여 flat 단어가 이름에 들어가게 되었습니다. 그렇지만 저는 map 함수는 구체타입을 이데아로 연결해 주는 함수이며 flatMap 은 이데아를 계속 거닐게 해주는 함수입니다. 라는 설명이 더욱 마음에 듭니다.
Result
infix fun <T, R> Result<T>.map(functor: (value: T) -> R): Result<R> {
return this.flatMap { value ->
Result.Success(functor(value))
}
}
infix fun <T, R> Result<T>.flatMap(functor: (value: T) -> Result<R>): Result<R> {
return when (this) {
is Result.Success -> {
functor(this.value)
}
is Result.Fail -> {
Result.Fail()
}
}
}
map 함수가 받는 functor는 구체타입 T를 받고 결과로 구체타입 R을 반환하는 람다입니다. 즉, 이 람다는 내부의 사이드이펙트가 없는 순수함수로 가정해야 합니다. 만약 사이드이펙트가 있는 함수는 함수 a처럼 구체타입을 받고 추상화된 모나드를 반환하는 함수로 정의해야 합니다. 다시 map 함수를 보면 내부에서 flatMap을 사용해 Result 모나드로 감싸고 있습니다. Success를 사용할 수 있는 이유는 functor가 순수함수라고 정의했기 때문입니다. 즉, 반환되는 구체타입을 map을 거치면 추상화된 모나드로 연결하여 주므로 map은 구체타입을 이데아로 연결해 주는 함수입니다.
flatMap을 보면 functor는 구체타입을 받고 결과로 모나드를 반환하는 람다입니다. 즉, 사이드이펙트가 존재할 수 있는 함수만을 받을 수 있습니다. 이전에 정의했던 함수 a처럼 내부에서 사이드이펙트를 모나드로 처리하여 순수함수성을 지키는 함수만 flatMap을 사용할 수 있고 결과는 계속해서 모나드로 이어지기 때문에 flatMap을 이데아를 거닐게 하는 함수로 볼 수 있는 것입니다.
map과 flatMap을 사용하여 합성해 봅시다. 방금 알아보았듯이 함수 a, d만 이용할 수 있습니다. 함수 b는 flatMap을 사용하여 표현할 수 있기 때문에 필요가 없습니다. 함수 c는 모나드에서 값을 추출하는 것이므로 계속 필요합니다. 함수 c의 이름을 쉽게 이해하기 위해서 value로 변경하겠습니다.
fun a(value: Int): Result<Int> {
if (value > 0) {
return Result.Success(value * 10)
} else {
return Result.Fail()
}
}
fun d(value: Int): Int {
return value * 10
}
fun value(value: Result<Int>): Int {
return when (value) {
is Result.Success -> {
value.value
}
is Result.Fail -> {
-1
}
}
}
합성해 보겠습니다.
val flow1 = a(10) map ::d flatMap ::a
println(value(flow1))
//출력
10000
원하는 결과를 얻었습니다. value 함수가 Int뿐 아니라 다른 타입에 대해서 동작하도록 Rx처럼 값을 얻게 Result
sealed class Result<T> {
data class Success<T>(val value: T): Result<T>()
class Fail<T>: Result<T>()
fun value(onSuccess: (T) -> Unit, onFailed: (Result.Fail<T>) -> Unit) {
return when (this) {
is Result.Success -> onSuccess(this.value)
is Result.Fail -> onFailed(this)
}
}
}
이제 합성식에 정수를 문자열로 바꾸는 연산을 추가해 봅시다.
val flow1 = a(10) map ::d flatMap ::a map { "SUCCESS :: $it" }
이 값을 출력해 봅시다.
flow1.value(
onSuccess = { println(it) },
onFailed = { println("failed")}
)
//출력
SUCCESS :: 10000
아주 쉽게 붙일 수 있습니다. 함수 $f$는 항상 Result.Fail을 반환하도록 작성해 봅시다.
fun <T> f(a: T): Result<T> {
return Result.Fail()
}
중간에 $f$를 합성해 보겠습니다.
val flow1 = a(10) map ::d flatMap ::f flatMap ::a map { "SUCCESS :: $it" }
flow1.value(
onSuccess = { println(it) },
onFailed = { println("failed")}
)
//출력
failed
원하는 대로 출력되었습니다. 다시 map과 flatMap을 봅시다.
infix fun <T, R> Result<T>.map(functor: (value: T) -> R): Result<R> {
return this.flatMap { value ->
Result.Success(functor(value))
}
}
infix fun <T, R> Result<T>.flatMap(functor: (value: T) -> Result<R>): Result<R> {
return when (this) {
is Result.Success -> {
functor(this.value)
}
is Result.Fail -> {
Result.Fail()
}
}
}
map은 내부에서 flatMap을 사용합니다. $f$가 Result.Fail을 반환하면 map 내부의 flatMap은 인자로 전달받은 functor에 상관없이 항상 Result.Fail을 반환합니다. flatMap은 Result.Success일 때만 functor를 실행함을 알 수 있습니다. 그래서 map 함수도 Result.Fail을 반환하게 되는 것입니다.
함수 합성을 통해서 데이터가 계속 흐르도록 하였습니다. 이제 2부에서 함수형 프로그래밍으로 작성한 프로그램을 왜 아래처럼 정의할 수 있는지 이해할 수 있을 것입니다.
\[클래스 = 데이터 + 로직\] \[타입 = { 원시타입, 클래스, 함수 }\] \[프로그램 = 타입 + 흐름\]3-6. 추상화와 문맥
3부를 마치기 전에 추상화와 문맥에 대해서 잠깐 살펴보려고 합니다. 4부에서는 다양한 모나드를 직접 구현해 보려고 합니다. 모나드는 왜 다양할까요? 그것은 추상화를 통해서 의미나 문맥을 담기 때문입니다. 말은 어렵지만 실제로는 쉽습니다.
우리가 코드를 작성하다 보면 값이 있을 수도 있고 없을 수도 있습니다. 그리고 때로는 비동기 실행도 필요합니다. 어떨 때는 A 또는 B를 선택해야 합니다. 이런 의미를 모나드가 담을 수 있는 것입니다.
\[f: X \rightarrow Maybe[Y]\]함수 $f$를 실행하면 Y 타입의 결과값이 있을 수도 있고 없을 수도 있습니다. 방금 우리는 함수 정의에 어떤 의미를 담았습니다!
\[g: P \rightarrow Future[Q]\]함수 $g$를 실행하면 Q 타입의 결과값을 지금이 아닌 미래의 어느 시점에 얻을 수 있음을 나타냅니다.
3-7. 정리
지금까지 배운 모나드를 정리하면 아래와 같습니다.
- 구체타입을 추상화한 타입
- 추상화 속엔 사이드이펙트도 포함할 수 있다.
- 사이드이펙트가 있는 함수를 순수함수로 바꾸어 주는 것
- map과 flatMap을 통한 함수 합성으로 데이터가 계속 흐를 수 있게 해 주는 것.
- 따라서 Monad는 Side Effect를 내포하면서 map과 flatmap을 정의한 타입
- 모나드는 문맥을 담는다.
4장. Monad 실전 예제
4부에서는 1부, 2부, 3부에서 배운 이론을 바탕으로 여러 모나드를 만들어 보겠습니다. 구현언어로 Kotlin을 사용하겠습니다.
4-1. Optional
Optional 모나드를 구현해 보겠습니다. Optional은 Swift, Kotlin에서 null이 가능한 타입입니다. 주로 Int? 처럼 구체타입에 ? 를 붙여서 표현합니다.
우선 타입과 map, flatMap을 정의합니다.
sealed class Optional<T> {
class None<T>: Optional<T>()
data class Some<T>(val value: T): Optional<T>()
}
infix fun <T, R> Optional<T>.map(functor: (value: T) -> R): Optional<R> {
return this.flatMap { value ->
Optional.Some(functor(value))
}
}
infix fun <T, R> Optional<T>.flatMap(functor: (value: T) -> Optional<R>): Optional<R> {
return when (this) {
is Optional.Some -> {
functor(this.value)
}
is Optional.None -> {
Optional.None()
}
}
}
Result 타입과 크게 다르지 않습니다. 정의한 Optional 모나드를 사용해 파일을 열고 콘텐츠인 텍스트 읽기를 구현해 보겠습니다.
fun testOptional() {
fun openFile(fileName: String): Optional<File> {
return try {
Optional.Some(File(fileName))
} catch (e: Throwable) {
Optional.None()
}
}
fun readFile(file: File): Optional<String> {
return try {
Optional.Some(file.inputStream().bufferedReader().use { it.readText() })
} catch (e: Throwable) {
Optional.None()
}
}
val content = openFile("greeting.txt") flatMap ::readFile
when (content) {
is Optional.Some -> println(content.value)
is Optional.None -> println("There is no file.")
}
}
위에서 우리는 파일을 열고 파일 내용을 반환하는 작업을 두 개의 함수로 나누었습니다. 함수가 단 하나의 역할만 하도록 잘게 쪼갠 것입니다. 이렇게 함수를 최소 단위로 나누면 단위 테스트가 쉬워져서 좋습니다. 그리고 유지보수도 쉬워집니다.
프로그램이 실행되는 곳에 greeting.txt 파일이 없다면 There is no file.이 출력될 것이고 파일이 있다면 파일의 내용이 출력될 것입니다. 아래와 같이 파일 내용을 만들어 greeting.txt 이름으로 파일을 저장합니다.
Hello! It's me!
다시 실행해 보면 이제는 파일의 내용이 출력되는 것을 확인할 수 있습니다. 만약 요구사항이 추가되어 모든 문자를 대문자로 출력하고 싶을 때는 어떻게 해야 할까요? map을 적용하면 그만입니다. 아래처럼 함수를 추가합니다.
fun testOptional() {
fun openFile(fileName: String): Optional<File> {
return try {
Optional.Some(File(fileName))
} catch (e: Throwable) {
Optional.None()
}
}
fun readFile(file: File): Optional<String> {
return try {
Optional.Some(file.inputStream().bufferedReader().use { it.readText() })
} catch (e: Throwable) {
Optional.None()
}
}
fun uppercase(value: String): String {
return value.toUpperCase()
}
val content = openFile("greeting.txt") flatMap ::readFile map ::uppercase
when (content) {
is Optional.Some -> println(content.value)
is Optional.None -> println("There is no file.")
}
}
아래처럼 출력됩니다.
HELLO! IT'S ME!
중요한 것은 기존 함수는 수정하지 않고 새로운 함수를 추가하여 문제를 해결한 점입니다. 함수를 잘게 나누어 프로그램을 개발하면 기존 로직의 수정과 삭제는 최대한 줄이고 새로운 함수만 추가하여 개발할 수 있습니다. 유지보수 문제가 무척 쉬워지는 것입니다.
4-2. Result
Result 모나드는 3부에서 만든 모나드입니다. Kotlin으로 만든 것은 이미 보았으므로 여기서는 Swift로 구현해 보겠습니다.
public enum Result<T> {
case success(T)
case fail
func map<R>(_ functor: (T) -> R) -> Result<R> {
return self.flatMap { value in
Result<R>.success(functor(value))
}
}
func flatMap<R>(_ functor: (T) -> Result<R>) -> Result<R> {
switch self {
case .success(let value):
return functor(value)
case .fail:
return Result<R>.fail
}
}
}
그리고 함수를 정의합니다.
func a(_ value: Int) -> Result<Int> {
if (value > 0) {
return .success(value * 10)
} else {
return .fail
}
}
func d(_ value: Int) -> Int {
return value * 10
}
합성을 적용해 봅니다.
public func testResultSuccess() {
let result = a(10).map(d).map(d).map(d).map { "\($0 * 10)" }
switch result {
case .success(let value):
print("SUCCESS :: \(value)")
case .fail:
print("failed")
}
}
public func testResultFail() {
let result = a(10).map(d).map(d).flatMap { a($0 * -1) }.map(d).map { "\($0 * 10)" }
switch result {
case .success(let value):
print("SUCCESS :: \(value)")
case .fail:
print("failed")
}
}
실행하면 결과가 출력됩니다.
testResultSuccess()
testResultFail()
//출력
SUCCESS :: 1000000
failed
4-3. Either
Either 모나드를 구현해 봅시다. Either는 Optional과 비슷한 모나드로 Left, Right 두 개의 집합을 갖습니다. Optional의 None이 Left에 그리고 Some이 Right에 매칭됩니다. Optional과 다른 점은 예외나 오류가 발생했을 때 Left에 해당 정보를 담을 수 있다는 점입니다. 그리고 Either 모나드가 Left일 때에는 합성이 더 진행되지 않고 멈춘다는 것입니다. 우리가 예외가 발생했을 때 함수의 실행을 멈추는 것과 동일합니다.
sealed class Either<out L, out R> {
data class Left<out L>(val value: L): Either<L, Nothing>()
data class Right<out R>(val value: R): Either<Nothing, R>()
}
infix fun <L, R, P> Either<L, R>.map(functor: (value: R) -> P): Either<L, P> {
return this.flatMap { value ->
Either.Right(functor(value))
}
}
infix fun <L, R, Q> Either<L, R>.flatMap(functor: (value: R) -> Either<L, Q>): Either<L, Q> {
return when (this) {
is Either.Left -> {
return Either.Left(this.value)
}
is Either.Right -> {
functor(this.value)
}
}
}
Either 모나드가 Left일 때 합성이 더 진행되지 않고 멈추는 이유는 flatMap 에서 Either.Right일 때만 functor를 실행하기 때문입니다. 예외가 발생했을 때 발생한 이후로 실행하지 않으려 할 때 Either를 사용하면 편리합니다.
테스트해 봅시다.
fun testEither() {
fun openFile(fileName: String): Either<Throwable, File> {
return try {
val file = File(fileName)
if (file.exists()) {
Either.Right(file)
} else {
Either.Left(FileNotFoundException())
}
} catch (e: Throwable) {
Either.Left(e)
}
}
fun readFile(file: File): Either<Throwable, String> {
return try {
Either.Right(file.inputStream().bufferedReader().use { it.readText() })
} catch (e: Throwable) {
Either.Left(e)
}
}
val content = openFile("greeting.txt") flatMap ::readFile
when (content) {
is Either.Left -> println(content.value)
is Either.Right -> println(content.value)
}
}
파일이 있다면 아래처럼 출력됩니다.
Hello! It's me!
파일이 없다면 아래처럼 출력됩니다.
java.io.FileNotFoundException: greeting2.txt (No such file or directory)
4-4. Future
Future 모나드는 비동기(async) 작업에 사용되는 모나드입니다. 비동기 작업(async task)은 동기 작업(sync task)과 다르게 값을 얻을 수 있는 시점을 알 수가 없습니다. 그래서 자주 사용되는 패턴이 Callback 패턴입니다. 비동기 작업이 완료되면 콜백을 호출해 값을 전해 줍니다. 그러나 콜백 패턴은 여러 비동기 작업을 체이닝하여 실행할 때 콜백지옥이 형성되어 코드 파악과 유지보수를 어렵게 합니다.
Future 모나드 사용하면 콜백지옥 없이 비동기 작업을 체이닝할 수 있습니다. Javascript의 Promise도 Future와 비슷한 모나드입니다.
여기서 구현하는 Future 모나드는 비동기 작업을 모나드로 추상화하는 개념을 보여주는 예제일 뿐입니다. 프로덕션 코드에 사용하시면 안 됩니다. :) 비동기 작업이 반환하는 값을 Future 모나드로 추상화하고 map과 flatMap으로 체이닝을 해 봅시다.
구현 아이디어는 아주 간단합니다. 사실 콜백 패턴을 그대로 따르고 있습니다. 내부에 콜백과 구독자(Subscribers) 목록을 가지고 있습니다. 비동기 작업이 끝나면 구독자에게 콜백을 사용해 값을 전달합니다.
우선 콜백타입을 정의합니다. 콜백은 Either 모나드를 사용해 오류 또는 값을 전달합니다.
typealias Callback<Err, T> = (Either<Err, T>) -> Unit
이제 비동기 작업을 실행할 스케줄러를 정의합니다. RxJava 스타일을 만들기 위해 정의한 것입니다. 별 의미는 없습니다.
interface Scheduler {
fun execute(command: () -> Unit)
fun shutdown()
}
object SchedulerIO: Scheduler {
private var executorService = Executors.newFixedThreadPool(1)
override fun execute(command: () -> Unit) {
if (executorService.isShutdown) {
executorService = Executors.newFixedThreadPool(1)
}
executorService.execute(command)
}
override fun shutdown() {
if (!executorService.isShutdown) {
executorService.shutdown()
}
}
}
object SchedulerMain: Scheduler {
override fun execute(command: () -> Unit) {
Thread(command).run()
}
override fun shutdown() = Unit
}
이제 Future 모나드를 구현해 봅시다. Future 모나드는 내부에 콜백 람다를 가지고 있습니다. 콜백이 실행되면 결과값을 cache에 담아 두었다가 모나드에서 구체타입의 값을 추출하는 subscribe에서 cache의 값을 사용합니다.
class Future<Err, V>(private var scheduler: Scheduler = SchedulerIO) {
var subscribers: MutableList<Callback<Err, V>> = mutableListOf()
private var cache: Optional<Either<Err, V>> = Optional.None()
var semaphore = Semaphore(1)
private var callback: Callback<Err, V> = { value ->
semaphore.acquire()
cache = Optional.Some(value)
while (subscribers.size > 0) {
val subscriber = subscribers.last()
subscribers = subscribers.dropLast(1).toMutableList()
scheduler.execute {
subscriber.invoke(value)
}
}
semaphore.release()
}
fun create(f: (Callback<Err, V>) -> Unit): Future<Err, V> {
scheduler.execute {
f(callback)
}
return this
}
fun subscribe(cb: Callback<Err, V>): Disposable {
semaphore.acquire()
when (cache) {
is Optional.None -> {
subscribers.add(cb)
semaphore.release()
}
is Optional.Some -> {
semaphore.release()
val c = (cache as Optional.Some<Either<Err, V>>)
cb.invoke(c.value)
}
}
return Disposable()
}
fun <P> map(functor: (value: V) -> P): Future<Err, P> {
return this.flatMap { value ->
Future<Err, P>().create { callback ->
callback(Either.Right(functor(value)))
}
}
}
fun <Q> flatMap(functor: (value: V) -> Future<Err, Q>): Future<Err, Q> {
return Future<Err, Q>().create { callback ->
this.subscribe { value ->
when (value) {
is Either.Left -> {
callback(Either.Left(value = value.value))
}
is Either.Right -> {
functor(value.value).subscribe(callback)
}
}
}
}
}
inner class Disposable {
fun dispose() {
scheduler.shutdown()
}
}
}
Future 모나드를 사용해 보기 위해서 비동기를 흉내 내는 count 함수를 정의합니다. 1초를 sleep하고 1을 증가시키는 함수입니다. 결과는 Future를 반환합니다.
fun count(n: Int): Future<Throwable, Int> {
return Future<Throwable, Int>().create { callback ->
Thread.sleep(1000)
callback.invoke(Either.Right(n + 1))
}
}
RxJava의 Single을 사용하는 것과 비슷합니다.
fun count(n: Int): Single<Int> {
return Single.create { emitter ->
Thread.sleep(1000)
emitter.success(n + 1)
}
}
count 함수를 사용하여 5까지 카운트를 하도록 체이닝을 해 보겠습니다.
fun testFuture(): Future<Throwable, Int> {
return Future<Throwable, Int>()
.create { callback ->
Thread.sleep(1000)
callback.invoke(Either.Right(1))
}
.flatMap(::count)
.map { it + 1 }
.flatMap(::count)
.flatMap(::count)
}
flatMap을 사용하여 비동기 작업을 계속해서 체이닝 할 수 있고 map을 사용하여 비동기 함수가 반환하는 값에 정적 스타일로 어떤 작업을 수행할 수 있음을 알 수 있습니다. 이 함수를 구독하는 함수는 아래와 같습니다.
fun main(args: Array<String>) {
val disposable = testFuture()
.subscribe {
when (it) {
is Either.Left -> print(it.value)
is Either.Right -> print(it.value)
}
}
Thread.sleep(5000L)
disposable.dispose()
val disposable2 = testFuture()
.subscribe {
when (it) {
is Either.Left -> print(it.value)
is Either.Right -> print(it.value)
}
}
Thread.sleep(5000L)
disposable2.dispose()
}
아래처럼 출력되고 프로그램이 종료됩니다.
5
5
Process finished with exit code 0
4-5. 정리
지금까지 여러 개의 모나드를 구현하고 사용해 보았습니다. 객체지향 시대에는 수많은 클래스와 함께했고 이제는 수많은 모나드와 함께하고 있습니다. 여러분도 함수의 인자 또는 결과를 구체 타입이 아닌 자신만의 모나드로 추상화해 보기를 권해 드립니다.
모나드를 정의하고 map가 flatMap을 만든 것은 흐름을 만들기 위함이었습니다. 실제로는 flatMap이 흐름을 만들어 줍니다. Either[Left, Right] 모나드를 구현할 때, Right일 때만 흐름이 진행되었습니다. 다시 Either 모나드 정의 코드를 보겠습니다.
sealed class Either<out L, out R> {
data class Left<out L>(val value: L): Either<L, Nothing>()
data class Right<out R>(val value: R): Either<Nothing, R>()
}
infix fun <L, R, P> Either<L, R>.map(functor: (value: R) -> P): Either<L, P> {
return this.flatMap { value ->
Either.Right(functor(value))
}
}
infix fun <L, R, Q> Either<L, R>.flatMap(functor: (value: R) -> Either<L, Q>): Either<L, Q> {
return when (this) {
is Either.Left -> {
return Either.Left(this.value)
}
is Either.Right -> {
functor(this.value)
}
}
}
위 코드에서 중요하게 기억해야 할 점은 flatMap에서 흐름을 진행할 타입에서 functor를 실행해 주는 것입니다. Either 모나드는 다른 Either 모나드가 Either.Right일 때만 아래처럼 흐름이 만들어집니다.
val content = openFile("greeting.txt") flatMap ::readFile map ::uppercase
자신만의 모나드를 만들 때 이점을 기억하면서 만들면 됩니다. 4부에서 구현한 모나드의 구현 코드는 Option/Maybe, Either, and Future Monads in JavaScript, Python, Ruby, Swift, and Scala 글의 내용을 참고한 것입니다. 이 글에는 JavaScript, Python, Ruby, Swift 그리고 Scala로 지금까지 살펴본 모나드 구현 코드를 볼 수 있습니다. 단, Kotlin으로 구현된 코드가 없어서 4부에서는 Kotlin을 중심으로 구현해 보았습니다.
5장. 함수형 아키텍처
4부까지 모나드의 개념을 알아보고 몇 개의 간단한 모나드를 구현해 보았습니다. 이런 질문을 가질 수도 있습니다. 이렇게 배운 모나드 개념이 실제로 앱을 개발하거나 웹앱 그리고 백앤드 서비스 등을 만들 때 도움이 될 수 있을까? 5부에서는 이 질문에 대한 답을 찾아보려고 합니다.
5-1. 프론트앤드 아키텍처
윈도우 운영체제가 GUI 운영체제로 일반 사용자들에게 익숙해져 있을 때, 개발자들은 MFC와 델파이의 VCL 프레임워크를 사용하여 윈도우용 프로그램을 개발했습니다. MFC는 Win32 API를 C++로 추상화한 프레임워크로 마이크로소프트가 개발하였고 VCL은 Win32 API를 Turbo Pascal로 추상화한 프레임워크로 볼랜드가 개발하였습니다. MFC는 Microsoft Foundation Class Library 의미였고 VCL은 Visual Component Library 의미였습니다. VCL은 그 이름답게 컴포넌트 개념을 정말 잘 표현한 라이브러리였습니다. Form이라는 바탕에 각종 컴포넌트를 드래그 앤 드롭으로 배치하고 각 컴포넌트를 서로 바인딩하여 코드 몇 줄만으로도 윈도우 앱을 만들 수 있었습니다. VCL을 만드신 분이 엔더슨 헤즐버그로 볼랜드 이후 마이크로소프트에서 C#과 Typescript를 만드신 분입니다.
윈도우 앱을 만들 때 많이 사용하던 아키텍처는 MVC 패턴이었습니다. 한동안 MVC 패턴은 프론트엔드 앱을 만들 때 사용하는 아키텍처가 되었습니다. MVC 패턴은 앱의 규모가 작을 때 사용하면 아주 좋은 아키텍처입니다. 왜냐하면 부가적인 코드가 거의 필요치 않기 때문입니다. 정의하려는 클래스가 Model, View 또는 Controller 중 어느 레이어에 포함되는지 구분하여 작성하면 되었고 컨트롤러에서 모델과 뷰를 함께 관리하여 앱을 만들 수 있었습니다.
시간이 흐르면서 통신의 속도가 빨라지고 콘텐츠의 용량이 커지고 플랫폼이 다양화되면서 앱의 규모는 커지게 되었습니다. 큰 규모의 앱에 MVC를 적용하다 보니 Controller의 규모가 커지게 되었습니다. Controller가 커지면서 자연스럽게 Controller 내부는 View와 Model이 서로 뒤엉켜 의존성을 높이는 결과를 낳았고 이는 유지보수를 어렵게 만들었습니다. 요즘은 MVC를 Massive View Controller 라 부르며 잘 사용하지 않는 아키텍처가 되었습니다. 사람들은 이 문제를 해결하기 위해서 다양한 아키텍처를 개발하게 되었습니다. MVP, MVVM, VIPER 등이 대표적으로 유명합니다.
이 아키텍처들의 공통점은 레이어 또는 모듈 간의 의존성을 최대한 제거하고 흐름을 단순하게 만드는 것이었습니다. 의존성을 제거하여 테스트를 쉽게 하고 교체를 쉽게 하고 변화에 쉽게 적응할 수 있도록 하는 것입니다. 다양한 아키텍처 중에서 이 글에서는 MVVM과 Redux를 살펴보며 함수형 아키텍처에 대해서 알아보려고 합니다.
5-1-1. MVP
MVVM 아키텍처는 MVP와 함께 모바일 앱 및 프론트 웹앱을 만들 때 많이 사용하는 아키텍처입니다. MVP와 MVVM을 사용하는 의사 코드를 살펴보면서 각 아키텍처를 살펴봅시다.
MVP는 Presenter에서 비즈니스 로직을 수행한 후 결과값을 인터페이스를 통해 View에 전달합니다. MVP는 Presenter에 View에 적용할 인터페이스를 매번 만들어줘야 해서 부가적인 코드가 많이 생성되는 단점이 있고 흐름이 단방향이 아니어서 앱의 규모가 커지면 흐름을 파악하기 어려운 단점이 있습니다. 경험으로는 인터페이스를 만들기 귀찮아서인지 View를 통째로 넘기는 코드도 많이 보았습니다.

interface UpdateView {
fun updateSomeProperty(value)
}
class View: UpdateView {
fun updateSomeProperty(value) {
this.someProperty = value
}
}
class Presenter {
fun requestSomeOutput(updater: UpdateView) {
val output = ... some business logic with models.
updater.updateSomeProperty(output)
}
}
controller {
val view = View()
val presenter = Presenter()
presenter.requestSomeOutput(view)
}
5-1-2. MVVM
MVVM은 단방향의 단순성 그리고 ViewModel의 출력을 바인딩을 통해 쉽게 사용할 수 있어 MVP보다 많이 사용되고 있는 것 같습니다. View의 속성과 ViewModel의 출력을 바인딩으로 연결해 놓고 ViewModel에 비즈니스 로직을 수행하도록 요청하면 ViewModel은 모델 및 서비스를 사용해 비즈니스 로직을 수행하고 결과를 출력으로 반환합니다. View의 속성과 ViewModel의 출력 바인딩을 통해 View는 자동으로 업데이트됩니다.

class View {
var someProperty
}
class ViewModel {
val someOutput
}
controller {
binding(view.somePropery, viewModel.someOutput)
viewModel.requestSomeOutput()
}
때로는 단방향이 아닌 양방향 바인딩이 사용되며 바인딩을 위한 코드 숨김이 심할 경우 디버깅이 어려워지는 단점이 있습니다. 맥 OS의 앱을 만드는 Cocoa가 대표적인 예로 양방향 바인딩을 사용하여 IDE 상에서 Model과 View를 양방향으로 바인딩하여 앱을 쉽게 작성할 수 있지만, 그 과정이 너무 숨겨져 있어 디버깅이 어려운 경우가 있습니다. 또한 안드로이드의 데이터 바인딩처럼 개발 편의를 위해서 바인딩 표현식에 약간의 로직과 수식을 지원할 때가 있습니다. 이 경우에는 해당 바인딩 표현식에 브레이크 포인터를 설정할 수 없기 때문에 실행 결과를 이해하기 위해서는 반드시 레이아웃 XML 파일을 직접 열고 바인딩 표현식을 읽어 봐야 합니다. 그래도 바인딩은 무척 편리하기 때문에 많이 사용되고 있습니다.
MVVM의 ViewModel을 다시 한번 살펴보면 흐름은 단방향이고 입력을 주면 출력을 반환하며, 바인딩을 통해서 자동으로 출력값이 View에 업데이트됩니다. ViewModel이 함수처럼 작동한다고 느껴집니다. 그러나 MVVM에서는 상태 변경을 항상 ViewModel을 통해서 이뤄지도록 강제하지 않기 때문에 여러 곳에서 상태 변경이 발생할 수 있고 View가 가진 상태값과 ViewModel이 가진 상태값이 다른 경우도 존재했습니다.
5-1-3. Redux
Flux는 페이스북에서 발표한 아키텍처이며 Redux는 Flux의 구현체로 Dan Abramov가 개발했습니다. Flux와 Redux에는 View, Action, Dispatcher, Store로 구성되어 있습니다. Flux와 Redux가 중요한 이유는 모든 상태를 Store에서 관리하고 Store에서 상태 변경(mutation)이 일어난다는 것입니다.
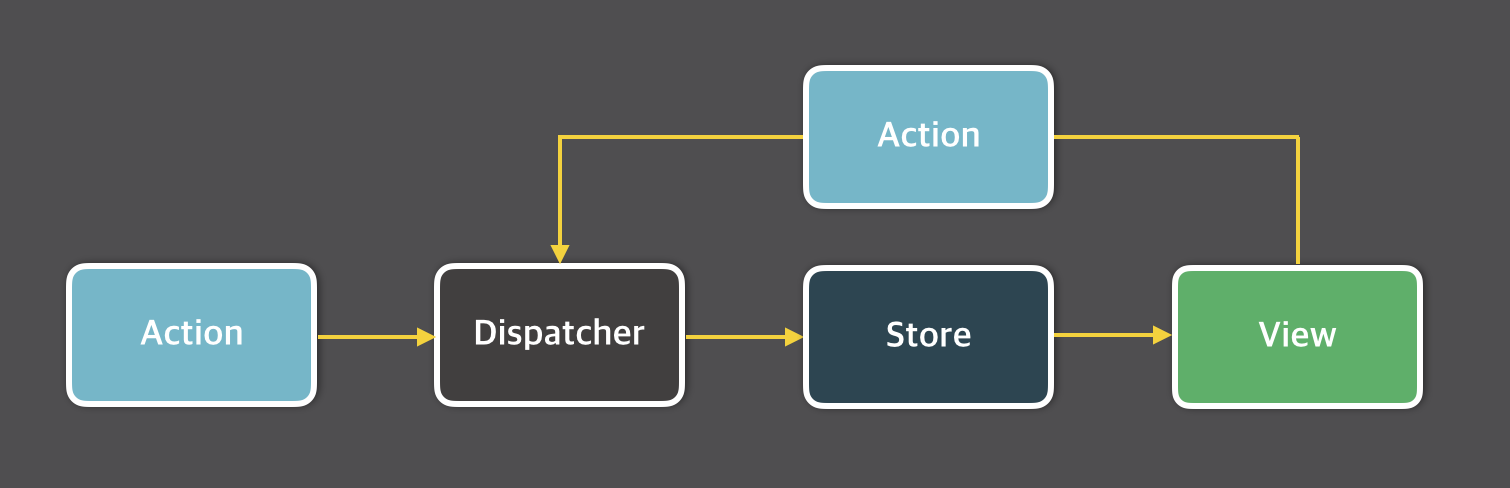
View는 Action을 Dispatcher를 통해 Store에 보내 비즈니스 로직을 요청합니다. Action을 사용하는 이유는 View가 최대한 약한 결합력을 갖추어 다른 모듈과의 디펜던시를 낮추기 위함입니다. React는 Component를 바탕으로 View를 구성하는 라이브러리로 Component를 최대한 독립적이고 재사용할 수 있게 만들어야 했기 때문에 의존성을 낮추는 것이 꼭 필요합니다. View는 자신이 보낼 Action과 자신을 그리기 위한 데이터만 알면 됩니다. 상태 변경이 항상 Store에서 이뤄지므로 View에는 Action을 보내고 새로운 상태가 오면 자신을 업데이트하는 코드만 있으면 충분합니다. 이를 그림으로 표현하면 아래와 같습니다.
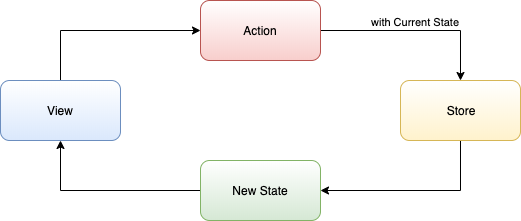
이 그림을 다시 생각해보면 View는 Store에 입력으로 Action과 현재 상태를 전달하고 Store에서 비즈니스 로직 및 서비스를 사용하여 새로운 상태를 만들어 결과로 반환합니다. 그리고 View는 새로운 상태에 반응해 자신을 업데이트합니다.
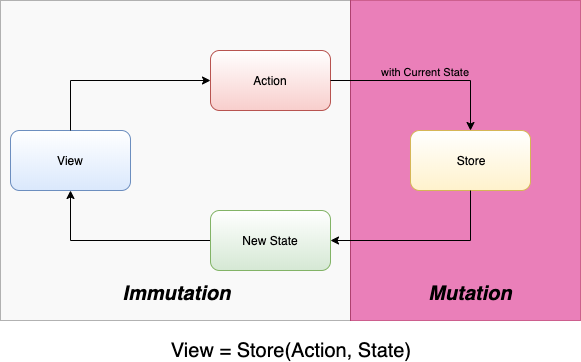
즉, Store는 함수가 됩니다. 이를 바탕으로 생각해 보면 Redux로 작성하는 앱은 아래와 같이 표현할 수 있습니다.
\[App = f \circ f \circ f \circ ... f \circ f \circ f(state)\]Redux는 입력과 출력을 Action과 State로 고정하고 Reducer를 통해서 Store에서만 Mutation이 되도록 하여 함수형 아키텍처가 됩니다. 함수형 아키텍처는 함수 합성을 통하여 확장하듯이 앱을 확장합니다. 클라이언트 앱에서 서버는 요청을 보내면 응답을 주는 서비스이며 서버에게 DB는 질의(Query)하면 데이터를 주는 서비스입니다. 모두 입력과 결과로 구성된 함수로 추상화할 수 있습니다.

아주 간단한 구조입니다. Server와 Database에서도 수많은 함수들이 합성되어 시스템을 구성할 것입니다. 함수를 합성하듯이 스택을 구성할 수 있습니다.
참고로 React Native와 함께 인기를 얻고 있는 Flutter는 UI를 아래처럼 정의하고 있습니다.

Apple은 SwiftUI로 그리고 Google의 Android는 Jetpack Compose로 Flutter와 React를 닮아가고 있습니다.
5-2. ReactComponentKit
ReactComponentKit은 iOS 및 Android 앱을 작성할 때, Redux 구조를 사용할 수 있는 아키텍처로 제가 만들고 관리하는 오픈소스입니다. 현재 iOS, Cocoa 그리고 Android 앱을 위한 라이브러리를 각각 제공하고 있습니다.
- https://github.com/ReactComponentKit/ReactComponentKit
- https://github.com/ReactComponentKit/AndroidReactComponentKit
- https://github.com/ReactComponentKit/CocoaReactComponentKit
실례로 안드로이드에서 Room을 사용하여 화면에 임의의 단어 목록을 추가, 삭제하는 앱을 살펴보겠습니다. 전체 코드는 HelloRoom에서 확인할 수 있습니다. 다음은 앱을 실행한 모습입니다.

5-2-1. Action
이 예제에서 필요한 Action은 아래와 같습니다.
// DB에서 저장된 모든 단어 목록을 로드합니다.
object LoadWordsAction: Action
// DB에 단어를 추가합니다.
data class InsertWordAction(val word: Word): Action
// DB에서 단어를 삭제합니다.
data class DeleteWordAction(val word: Word): Action
5-2-2. Component
Action을 보내는 컴포넌트는 아래와 같습니다.
interface WordProvider {
val word: Word
}
data class WordModel(override val word: Word): ItemModel(), WordProvider {
override val componentClass: KClass<*>
get() = WordComponent::class
override val id: Int
get() = word.hashCode()
}
class WordComponent(token: Token): ViewComponent(token) {
private lateinit var textView: TextView
override fun layout(ui: AnkoContext<Context>): View = with(ui) {
val view = include<View>(R.layout.word_component)
textView = view.findViewById(R.id.textView)
return view
}
override fun on(item: ItemModel, position: Int) {
val wordProvider = (item as? WordProvider) ?: return
textView.text = wordProvider.word.word
}
}
이 컴포넌트는 단순히 단어를 화면에 표시만 합니다. 자신이 사용할 데이터 이외에는 이 컴포넌트는 다른 모듈과 디펜던시가 없습니다.
5-2-3. Reducers
각 액션을 받으면 상태를 수정할 Reducer입니다.
// DB에서 저장된 모든 단어 목록을 로드합니다.
fun MainViewModel.loadWords(state: MainViewState): MainViewState {
val words = WordDB.getInstance(getApplication())
.wordDao()
.getAlphabetizedWords()
return state.copy(words = words)
}
// DB에 단어를 추가합니다.
fun MainViewModel.insertWord(state: MainViewState, action: InsertWordAction): MainViewState {
WordDB.getInstance(getApplication())
.wordDao()
.insert(action.word)
return state
}
// DB에서 단어를 삭제합니다.
fun MainViewModel.deleteWord(state: MainViewState, action: DeleteWordAction): MainViewState {
WordDB.getInstance(getApplication())
.wordDao()
.delete(action.word)
return state
}
모든 상태 변경 코드는 백그라운드에서 실행되어 Room을 위처럼 사용할 수 있습니다. 그리고 변경된 상태를 WordComponent를 통해 RecyclerView에 표시하기 위해서 WordComponent를 위한 WordModel을 생성합니다.
// Make ItemModels from word list for the recycler view
fun MainViewModel.makeItemModels(state: MainViewState): MainViewState {
val itemModels = state.words.map { WordModel(it) }
return state.copy(itemModels = itemModels)
}
지금까지 살펴본 Reducer는 단 하나의 책임만 가지고 있어 코드를 파악하기 쉽습니다.
5-2-4. State
예제 앱을 위한 상태를 정의합니다. ReactComponentKit은 Activity, Fragment 또는 UIViewController 마다 State를 관리하도록 했습니다. 그 이유는 Android와 iOS 앱은 React와 달리 Single Page App이 아닙니다. 그리고 같은 화면이 내비게이션 스택에 다른 상태를 가지고 여러 번 등장할 수 있기 때문에 각 화면이 자신의 상태를 갖는 것이 합리적이라고 판단했습니다.
data class MainViewState(
val words: List<Word> = emptyList(),
val itemModels: List<WordModel> = emptyList()
): State() {
override fun copyState(): MainViewState {
return copy()
}
}
5-2-5. ViewModel
위에서 정의한 상태를 ViewModel에서 관리합니다. ReactComponentKit은 Store와 함께 ViewModel을 사용하고 있습니다. ViewModel은 입력된 Action에 어떻게 반응하는지 기술하고 출력값을 Output으로 관리합니다.
class MainViewModel(application: Application): RCKViewModel<MainViewState>(application) {
val itemModels = Output<List<WordModel>>(emptyList())
override fun setupStore() {
initStore { store ->
store.initialState(MainViewState())
store.flow<LoadWordsAction>(
{ state, _ -> loadWords(state) },
{ state, _ -> makeItemModels(state) }
)
store.flow<InsertWordAction>(
::insertWord,
{ state, _ -> loadWords(state) },
{ state, _ -> makeItemModels(state) }
)
store.flow<DeleteWordAction>(
::deleteWord,
{ state, _ -> loadWords(state) },
{ state, _ -> makeItemModels(state) }
)
}
}
operator fun get(index: Int): Word = withState { state ->
state.words[index]
}
override fun on(newState: MainViewState) {
itemModels.accept(newState.itemModels)
}
override fun on(error: Error) {
Log.e("MainViewModel", error.toString())
}
}
initStore 함수에서 각 액션에 대한 mutation 흐름을 기록해 놓아 코드 파악을 쉽게 하였습니다. 예제 코드에는 없지만, 비동기 mutation을 flow에 쉽게 담기 위해 awaitFlow도 지원합니다. 또한 asyncFlow와 nextDispatch도 지원합니다.
새로운 상태는 on(newState:)메서드로 전달되며 flow를 실행하다 발생한 오류는 on(error:)한 곳으로 전달됩니다. MainViewModel은 Action을 인자로 받고 Output 또는 Error를 반환하는 함수로 생각할 수 있습니다.
5-2-6. Controller(MainActivity)
Controller 역할을 하는 Activity의 코드는 아래와 같습니다.
class MainActivity : AppCompatActivity() {
private lateinit var viewModel: MainViewModel
private val disposeBag: AutoDisposeBag by lazy {
AutoDisposeBag(this)
}
private val layoutManager: LinearLayoutManager by lazy {
LinearLayoutManager(this, RecyclerView.VERTICAL, false)
}
private val adapter: RecyclerViewAdapter by lazy {
RecyclerViewAdapter(token = viewModel.token, useDiff = true)
}
private val itemTouchHelper: ItemTouchHelper by lazy {
ItemTouchHelper(SwipeToDeleteCallback {
val word = viewModel[it]
viewModel.dispatch(DeleteWordAction(word))
})
}
override fun onCreate(savedInstanceState: Bundle?) {
super.onCreate(savedInstanceState)
setContentView(R.layout.activity_main)
setSupportActionBar(toolbar)
viewModel = ViewModelProviders.of(this).get(MainViewModel::class.java)
// 어댑터에 사용할 컴포넌트를 등록합니다.
adapter.register(WordComponent::class)
recyclerview.layoutManager = layoutManager
recyclerview.adapter = adapter
itemTouchHelper.attachToRecyclerView(recyclerview)
loadWords()
handleClickEvents()
handleViewModelOutputs()
}
private fun loadWords() {
viewModel.dispatch(LoadWordsAction)
}
private fun handleClickEvents() {
fab.onClick {
val word = Word(WordUtils.randomWord)
viewModel.dispatch(InsertWordAction(word))
}
}
private fun handleViewModelOutputs() {
viewModel
.itemModels
.asObservable()
.subscribe {
adapter.set(it)
}
.disposedBy(disposeBag)
}
}
MainActivity가 실행될 때, LoadWordsAction을 보냅니다. 그리고 FAB 버튼을 누르면 랜덤으로 단어를 생성하여 InsertWordAction(word)을 보냅니다. 스와이프 제스처를 실행하면 DeleteWordAction(word)을 보냅니다. 각 액션에 대해 ViewModel과 Store가 비즈니스 로직 및 서비스를 실행하여 새로운 상태를 만들고 새로운 상태는 viewModel의 itemModels라는 Output으로 출력되어 RecyclerView를 업데이트합니다. RecyclerView는 내부에서 WordComponent에 WordModel을 전달하여 컴포넌트가 자신을 업데이트할 수 있습니다. ViewModel과 Store에는 Action과 현재 상태가 입력되고 새로운 상태가 출력됩니다. 그리고 Reducer는 잘게 나누어 쉽게 확장이 가능토록 할 수 있습니다.
5-3. 정리
React와 Redux를 네이티브 앱에 도입한 오픈소스 아키텍처는 ReactComponentKit 이외에도 많습니다. AirBnB의 Epoxy와 MvRx 그리고 ReactorKit 등이 있습니다.
- https://github.com/airbnb/MvRx, https://github.com/airbnb/epoxy
- https://github.com/ReactorKit/ReactorKit
6장. 부록
6-1. 타입 캐스팅 - C언어 타입 캐스팅이 위험한 이유
타입을 집합이라고 했을 때, C언어의 타입 캐스팅 연산자가 왜 위험한지 알 수 있습니다. 그리고 모던 프로그래밍 언어에는 타입 캐스팅 연산자가 왜 여러 개가 존재하는지 알 수 있습니다.
C언어의 타입 캐스팅은 아래와 같습니다.
int ch = (int)'a';
문자형인 char 타입에서 정수형인 int 타입으로 타입 캐스팅을 하였습니다. C언어의 타입 캐스팅은 가장 강력하면서도 무식한 연산자입니다. 강력하면 좋을 것 같은데 왜 위험한 것일까요? 다음 예제를 보겠습니다.
사람은 죽는다.
소크라테스는 사람이다.
고로 소크라테스는 죽는다.
위 삼단 논법은 논리가 명확합니다. 윗글이 어떤 프로그램이라고 할 때, C언어의 타입 캐스팅을 적용해 보겠습니다.
돌맹이 = (돌맹이)소크라테스
사람은 죽는다.
돌맹이는 사람이다.
고로 돌맹이는 죽는다.
어떤가요? 말도 안 된다는 것을 알 수 있습니다. 즉, C언어의 타입 캐스팅은 프로그래밍 언어의 근간인 논리를 파괴하는 연산자입니다. 타입 캐스팅을 잘 못 하면 프로그램이 크래시가 발생하는 것은 부차적입니다. 프로그래밍은 논리의 언어인데 이 논리를 파괴하는 것이 더 큰 문제입니다. C언어가 이렇게 만들어진 이유는 오직 성능 때문입니다. 모던 프로그래밍 언어는 다양한 타입 캐스팅 연산자를 제공해 개발자가 프로그램의 논리를 파괴하지 않도록 도와줍니다. Kotlin만 보아도 as, is 그리고 toInt(), toString() 등 다양한 타입 캐스팅 연산자를 제공합니다. 그리고 각 타입 캐스팅 연산자마다 용도와 때가 정해져 있습니다. C언어처럼 A타입에서 B타입(예: Int와 Long) 간에 자동으로 캐스팅이 되는 경우는 없습니다.
6-2. 이항연산과 컴퓨터 프래그래밍
$1 + 45^{\circ}$은 이항 연산이 아닙니다. 수학의 이항 연산은 같은 집합의 두 원소 간의 연산이기 때문입니다. 따라서 $1 + 45^{\circ}$을 계산하려면 각도 집합으로 통일하던가 아니면 실수 집합으로 통일해서 연산해야 합니다. 컴퓨터 프로그래밍의 연산도 이러한 성질을 따릅니다. 서로 다른 타입 간에 연산은 정의되지 않는 것이 원칙입니다. C언어에서 정수 int 타입과 실수 Double 타입 간에 + 연산이 수행되는 이유는 정수 int 타입이 자동으로 Double 타입으로 변환되어 연산 되기 때문입니다. 하지만 이런 자동 형 변환은 좋지 않은 것이기 때문에 모던 프로그래밍 언어에서는 모두 직접 명시적으로 형 변환을 수행토록 하는 추세입니다.
6-3. 빌더패턴, 제네릭과 흐름
6-3-1. 빌더패턴과 흐름
이 글에서 살펴본 데이터의 흐름은 익숙한 모양새입니다. C++를 배웠다면 iostream의 입출력 연산자를 아래처럼 사용하는 것이 익숙할 것입니다.
std::cout << 1 << "2" << 3.0 << std::endl
이렇게 쓸 수 있는 이유는 << 연산자가 this 포인터를 반환하기 때문입니다. 그래서 this 포인터 체이닝을 구성할 수 있습니다. 이와 비슷한 패턴은 Builder 패턴입니다.
val builder = SomeType.Builder()
builder
.setSomeValue(x)
.set....
.set....
.set...
.build()
빌더 패턴도 마찬가지로 각 메서드가 this포인터를 반환하여 위처럼 흐름을 구성할 수 있습니다. 모나드와 차이점은 this 포인터가 흐르는 것은 언제나 사이드이펙트가 발생할 수 있음을 암시하는 것입니다. 사이드이펙트를 줄이는 모나드와 달리 this 포인터를 흐르게 하는 것은 사이드이펙트를 부풀리는 것입니다.
6-3-2. 제네릭과 함수 합성
함수 합성식을 보면 모든 함수의 인자와 결과값을 제네릭 타입으로 설정하면 될 것처럼 느껴집니다.
fun <T> a(value: T): T
fun <T> b(value: T): T
fun <T> c(value: T): T
val result = c(b(a))
그러나 위처럼 할 수 없습니다. 그 이유는 제네릭은 타입의 정보를 지우는 것에서 출발합니다. 함수 a, b, c의 내용을 정의하려고 해도 타입 T가 클래스인지 원시타입인지 사칙 연산자는 지원하는지 등을 알 수 없기 때문에 함수를 정의할 수 없습니다. 모나드 Monad[T]는 감싸는 타입은 제네릭 타입이지만 자신의 타입은 그대로 유지합니다. 그리고 map과 flatMap을 실행할 때는 Monad[T]가 특정 타입으로 구체화 되어 있기 때문에 람다를 통해서 구체타입의 정보를 알 수 있어 원하는 연산을 수행할 수 있습니다.
글을 마치며
지금까지 긴 글을 읽어 주셔서 감사합니다. 부족한 글이지만 모나드를 이해하는데 도움이 되었기를 바래봅니다. 수정할 내용 또는 피드백이 있으시다면 sungcheol@dable.io 또는 skyfe79@gmail.com으로 보내주세요. 감사합니다.