광고 CTR 예측: FFM
Dable 처럼 광고플랫폼을 서비스하는 회사들은 어떤 광고 캠페인에 대한 CTR(click-through rate)을 정확하게 예측하는 것이 매우 중요합니다. 더 나아가 CR(conversion rate)도 예측 할 수 있다면 광고 효율을 높이는 데에 큰 도움이 될 것입니다.
광고가 보여질 특정 환경이 주어 졌을 때 { 광고가 보여지는 지면, 사용자, 사용자의 정보, 시간, 광고가 보여지는 지면(기사)의 내용, 광고 캠페인, etc… } 주어진 환경에서 노출 가능한 광고 캠페인이 100개 존재한다고 가정하면, 이 100개의 광고들 중 가장 CTR이 높을 것 같거나, CR이 높을 것 같은 광고를 노출시켜 줄 수 있다면 우리는 높은 광고 효율을 달성 할 수 있을 것입니다.
\[P_{ctr}=P(click|ad\ campaign, media, channel, user, time, ...)\] \[P_{cr}=P(conversion|click, ...)\cdot P_{ctr}\]자, 그렇다면 $P_{ctr}$ 을 예측하기 위해서는 어떤 모델을 사용해야 할까요? 보통 아래 나열한 모델들을 사용하는 것이 가장 효과적이다 라고 알려져 있습니다.
- LR (Logistic regression)
- FTRL-Proximal (Follow the regularized leader)
- FM (Factorization machines)
- FFM (Field-aware factorization machines)
- GBDT (Gradient boosted decision trees)
- Deep-NN
물론 시시각각 변화하는 사용자들의 반응이나 지면, 광고의 변화를 실시간으로 반영하기 위해서는 온라인으로 학습이 가능한 모델을 선택해야 합니다. 광고에는 새로운 유형의 오디언스가 계속 등장하고, 새로운 광고주와 광고 소재가 등록 또는 폐기되며, 새로운 성향의 매체 지면이 추가되는 것이 빈번하기 때문입니다. 이러한 환경적인 변화를 실시간으로 반영하지 못한다면 정확한 예측은 힘들 것 입니다.
오늘은 위에서 나열한 모델들 중 상당히 높은 정확도와 온라인 학습으로 확장이 가능한 모델인 FFM에 대해 다루도록 하겠습니다. FFM의 경우 여러 번 Kaggle에서 주최하는 CTR 예측 대회에서 이긴 경력이 있습니다. 어떻게 이렇게 정확한 예측을 할 수 있었던 것일까요? 한번 필자가 조아라하는 deep-dive를 해보도록 하겠습니다.
Dataset
실제 예측모델을 프러덕션 수준으로 적용하기 위해서는 안정적인 데이터 파이프라인 구축, 데이터 전처리 작업을 통한 노이즈 제거, 어뷰징 데이터 제거, 중복 제거, 정규화, 샘플링, categorical 필드 처리 등의 여러 사전 작업이 필요합니다. 하지만 여기서 이런 내용을 다루지는 않겠습니다. (사실 이런 전처리 작업들이 전체 작업의 80% 이상을 차지합니다. oops~)
이런 전처리 작업이 완료된 뒤 학습에서 사용될 데이터에 대한 예를 들어보면 아래와 같을 것입니다.
| is_clicked? $y(\vec{x})$ | male | female | PC | mobile | media1 | media2 | campaign1 | campaign2 | programmer | … |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | … |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | … |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | … |
위의 예시 데이터의 경우 모든 feature들은 categorical type이며, 이를 one-hot encoding으로 풀어서 표현하였습니다. one-hot encoding의 특징상 위 dataset 은 feature 차원이 상당히 크며(>$10^4$) sparse 할 것입니다.
From linear model to FM and FFM
Linear model
FFM을 소개하기에 앞서 단순한 선형 모델부터 차근차근 설명하도록 하겠습니다. 일반적인 linear model은 아래와 같은 수식으로 표현됩니다.
\[f(X) = w_0 + \sum_{i=1}^{n}w_ix_i \tag{1}\]linear model은 컴퓨팅 비용이 적기 때문에 대용량의 데이터셋을 빠르게 학습 시킬 때 효과적입니다. 광고 action 로그의 경우 분당 수억 건의 action이 발생하기 때문에 컴퓨팅 비용을 생각한다면 이처럼 단순한 모델이 적합하다고 할 수 있겠습니다. 하지만 위 모델을 실제 데이터를 가지고 학습을 시켜 보면 높은 feature 차원, 무시된 feature 간의 상관관계, 높은 sparsity와 선형적으로 구분하기 힘든 복잡도 등의 이유로 예측 정확도가 낮게 됩니다.
이를 보완하기 위해서는 nonlinear model인 kernel SVM, GDBT, deep-NN 등을 사용하거나, 아니면 단순히 linear model을 degree-2 polynomial combination(Poly2) 로 확장하여 아래와 같이 수정할 수 있습니다.
\[f(X) = w_0 + \sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}w_{ij}x_ix_j\]- $f(X)$는 is_clicked에 대한 예측값
- $w_0$는 bias term : $w_0 \in \mathbb{R}$
- $w_i$는 각 feature에 대한 가중치 : $\vec{w} \in \mathbb{R}^n$
- $w_{ij}$는 두 feature $x_i, x_j$ 곱(상관관계)에 대한 가중치 : $\vec{w} \in \mathbb{R}^{n^2}$
이렇게 2차원의 feature간의 상관관계를 고려하게 되면 예를 들어 ‘male’과 ‘programmer’ 가 조합 되었을 때 ‘PC’에서 광고를 클릭할 확률이 높다는 것이 학습이 가능해집니다. 해당 모델에서 필요한 parameter의 수는 $O(n^2)$ 이며 m 차원까지 고려하게 되면 parameter의 수는 $O(n^m)$로 급격하게 증가하게 됩니다. 따라서 parameter 증가로 인한 비용 증가와 feature들의 극심한 sparsity 등의 문제는 해당 모델에서 해결할 수 없을 것입니다.
Factorization Machines
아래 수식은 degree=2 일때의 FM 수식을 나태냅니다.
\[f(X) = w_0 + \sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}(\vec{v}_i \cdot \vec{v}_j)x_ix_j \tag{2}\]- $n$ : number of features
- $w_0 \in \mathbb{R}$
- $\vec{w} \in \mathbb{R}^n$
- $\textbf{V} \in \mathbb{R}^{n \times k}$
$\vec{v_i} \cdot \vec{v_j}=\sum_{f=1}^{k}v_{i,f} v_{j,f}$
- $k$ : number of factors
- $\hat{w}_{i,j}:=\vec{v_i} \cdot \vec{v_j}$ $i$번째 feature와 $j$번째 feature간의 상관관계를 모델링함
위 수식에 나타나 있듯이 FM은 linear model과는 다르게 두 feature 간의 상관관계를 독립된 하나의 값인 $w_{ij}$ 로 나타내기보다는 $k$차원으로 factorizing 된 두 벡터의 내적으로 표현합니다. 따라서 $\textbf{V}$에 포함된 한 row인 $v_i$는 $k$ factor로 확장된 $i$번째 feature를 나타냅니다.
이렇게 되면 linear model에서 이슈된 극심한 sparsity 때문에 예측이 실패하는 문제를 완화 시킬 수 있습니다. 예를 들어 linear model에서는 train 시점에 PC = 1과 campaign1 = 1 인 경우에 대한 data가 존재하지 않았다면 이 둘의 상관관계를 표현하는 $w_{ij}$는 그저 0이라고 학습될 것입니다. 하지만 FM의 경우에는 PC와 campaign1 feature를 $k$-차원의 벡터로 embedding 시켜 더 많은 정보를 담게 해주었기 때문에 만약 직접적인 연관성이 train data 상에서 보이지 않더라도 간접적으로 연관성이 존재하면 해당 정보가 담아지게 됩니다.
다시 예들 들어보면 비록 train 시점에 PC = 1과 campaign1 = 1인 경우에 대한 data가 존재하지 않았지만, PC = 1과 programmer = 1인 경우와 campaign1 = 1과 programmer = 1인 경우의 data가 존재한다면 결국 PC = 1과 campaign1 = 1의 상관관계를 간접적으로나마 알 수 있을 것입니다. $\textbf{V}$는 이러한 정보들을 담게 됩니다. 이미 알려진 SVD의 개념과 별반 다르지 않지만 아름답게 느껴집니다.
자 이제 두 feature 간의 상관관계를 d개의 feature 간의 상관관계로 확장시켜 봅시다. degree=d 로 일반화된 FM 수식은 아래와 같습니다.
$f(X) = w_0 + \sum_{i=1}^{n}w_ix_i+\sum_{l=2}^{d}\sum_{i_1=1}^{n}…\sum_{i_l=i_{l-1}+1}^{n} ( \prod_{j=1}^{l}x_{i_j})(\sum_{f=1}^{k_l}\prod_{j=1}^{l}v_{i_j,f}^{(l)})$
- $\textbf{V}^{(l)} \in \mathbb{R}^{n \times k_l}$, $k_l \in \mathbb{N}_0^+$
하지만 보통 CTR 예측할 때 degree=2 에서 거의 수렴된 예측 정확도를 얻을 수 있기 때문에 비용이 크게 증가하는 3차까지 가는 경우는 드뭅니다. 2차일 때의 계산 비용은 $O(nk)$ 지만 d차 일 때는 $O(k_dn^d)$로 급격하게 증가하기 때문입니다.
여기서 몇몇 분들은 2차 일때의 비용을 보고 의구심이 들것입니다. 분명 수식 $(2)$를 보면 계산 비용이 $O(n^2k)$ 인데 $O(nk)$ 라고 하였으니 말이죠. 그 이유는 아래와 같이 수식 $(2)$를 풀어 쓸 수 있기 때문입니다.
\[\begin{aligned} \sum_{i=1}^{n}\sum_{j=i+1}^{n}(\vec{v}_i \cdot \vec{v}_j)x_ix_j &= \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}(\vec{v}_i \cdot \vec{v}_j)x_ix_j - \frac{1}{2}\sum_{i=1}^{n}(\vec{v}_i \cdot \vec{v}_i)x_ix_i \\ &= \frac{1}{2}\left(\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{f=1}^{k}v_{i,f}v_{j,f}x_ix_j - \sum_{i=1}^{n}\sum_{f=1}^{k}v_{i,f}v_{i,f}x_ix_i\right) \\ &= \frac{1}{2}\sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n}v_{i,f}x_i\right)\left(\sum_{j=1}^{n}v_{j,f}x_j\right)-\sum_{i=1}^{n}v_{i,f}^2x_i^2\right) \\ &= \frac{1}{2}\sum_{f=1}^{k}\left( \left( \sum_{i=1}^{n}v_{i,f}x_i \right)^2 - \sum_{i=1}^{n}v_{i,f}^2x_i^2 \right) \end{aligned}\]더 나아가 우리가 다루는 data는 sparsity가 상당히 높기 때문에 계산 시 $x_i$가 0이 아닌 feature만 sum에 포함되어 실제 비용은 $O(k\overline{n})$로 줄어들게 됩니다. 여기서 $\overline{n}$는 0이 아닌 값들의 개수에 대한 평균값입니다.
이번에는 $k$에 대해 좀 더 고민해 보겠습니다. Linear algebra를 들여다보면 feature들 간의 상관관계를 담고 있는 어떤 positive definite matrix $\textbf{W}$는 nonsingular matrix $\textbf{V}$ 로 분해될 수 있습니다. $\textbf{W}=\textbf{V}\textbf{V}^t$ 이때 square matrix인 $\textbf{V}$를 $k$ dimension으로 approximation 할 수 있습니다. 물론 $k$ 값이 충분히 큰 값이어야 손실이 적을 것 입니다. 보통 $k$값은 cross-validation을 통해 적절한 값을 찾게 됩니다.
자 마지막으로 FM 학습 시 사용되는 방법론에 대해 설명드리겠습니다. 위에서 보았듯이 FM 모델은 linear time에 계산되는 closed formula를 얻게 됩니다. 따라서 online-learning에 종종 사용되는 SGD(stochastic gradient descent) 알고리듬을 이용하여 효과적으로 학습 할 수 있습니다. 이때 사용되는 loss function은 square, logit, hinge loss 등이 사용될 수 있을 것이며, 아래는 CTR 예측에 일반적으로 사용되는 logistic loss function을 보여줍니다.
$logloss = \frac{1}{m}\sum_{i=1}^{m}log(1+exp(-y_i\phi (\vec{w}, \textbf{V}, \vec{x})))$
여기에 필요하다면 regularization term을 추가할 수 있을 것 입니다. SGD를 위해 gradient를 구해보면 아래와 같습니다. \(\begin{aligned} \frac{\partial }{\partial\theta }\hat{y}(\vec{x}) = \left\{\begin{matrix} 1, & if\ \theta \ is\ w_0 & \\ x_i, & if\ \theta \ is\ w_i & \\ x_i\sum_{j=1}^{n}v_{j,f}x_j - v_{i,f}x^2_i, & if\ \theta \ is\ v_{i,f} & \end{matrix}\right. \end{aligned}\)
여기서 $\sum_{j=1}^{n}v_{j,f}x_j$ 은 $i$와 무관하기 때문에 사전에 계산할 수 있습니다. 일반적으로 gradient 계산 비용은 $O(1)$ 이며 모든 parameter들을 한번 갱신하는 데 드는 비용은 $O(kn)\ or\ O(k\overline{n})$ 일 것입니다. 자, 이제 FM은 마스터하였으니 FFM으로 넘어가 보도록 하겠습니다.
Field-aware Factorization Machines
degree=2 에서의 FFM 수식은 아래와 같습니다. FM과 비교했을 때 크게 달라 보이지는 않습니다.
\[f(X) = w_0 + \sum_{i=1}^{n}w_ix_i+\sum_{i=1}^{n}\sum_{j=i+1}^{n}(v_{i,f_j} \cdot v_{j,f_i})x_ix_j \tag{3}\]달라진 것이라곤 $(\vec{v_i} \cdot \vec{v_j})$ 가 $(\vec{v_{i,f_j}} \cdot \vec{v_{j,f_i}})$ 로 바뀐 것뿐입니다. 여기서 $f_i$의 의미는 $x_i$가 포함된 field의 정보이며 $f_j$는 마찬가지로 $x_j$가 포함된 field의 정보입니다. 예를 들어 광고 캠패인 field에는 A, B, C, D 라는 캠패인이 포함되어 있고 성별 field에는 M, F가 있다고 한다면, FFM에서는 FM과는 다르게 서로 다른 feature 간의 상관관계를 계산할 때 상대방 feature에 대한 field 정보를 추가적으로 고려해 줍니다. 즉, 캠패인 A와 성별 M 간의 상관관계를 표현하는 factorize 된 k 차원의 latent vector는 $\vec{v_{campaignA,field_gender}}$와 $\vec{v_{gnederM,field_campaign}}$ 가 되어 dot product로 두 feature 간의 상관관계를 계산하게 됩니다. 마찬가지로 만약 캠패인 A와 연령 Z 간의 상관관계를 계산한다면 $\vec{v_{campaignA,field_age}}$와 $\vec{v_{ageZ,field_campaign}}$ 의 dot product로 계산됩니다.
이와 같은 원리로 FM에서는 다른 field와의 모든 상관관계를 동일한 k 차원의 latent vector로 rough 하게 일반화(under-fitting) 시켰다면 FFM에서는 $\textbf{V}$에 field 정보를 포함시켜 $\times f$ 차원 확장하여 필드 간의 상관관계도 고려해 줍니다. 하지만 파라미터의 수가 $nfk$개로 증가하여 dataset이 크지 않다면 overfitting의 위험이 존재합니다. 물론 FFM의 컴퓨팅 비용도 $O(k\overline{n}^2)$로 증가하게 됩니다. 결국 우리는 구글이 아닌 이상 경우에 따라 적절한 모델을 선택하여 사용해야 할 것입니다. 혹은 비용의 제약이 없다면 앙상블, stacking 등의 방법론을 적용하여 좀 더 잘 일반화시켜 예측 정확도를 높일 수도 있을 것입니다. 아래 그림은 linear model, FM, FMM 간의 파라미터 차원의 차이를 도식적으로 보여주고 있습니다.
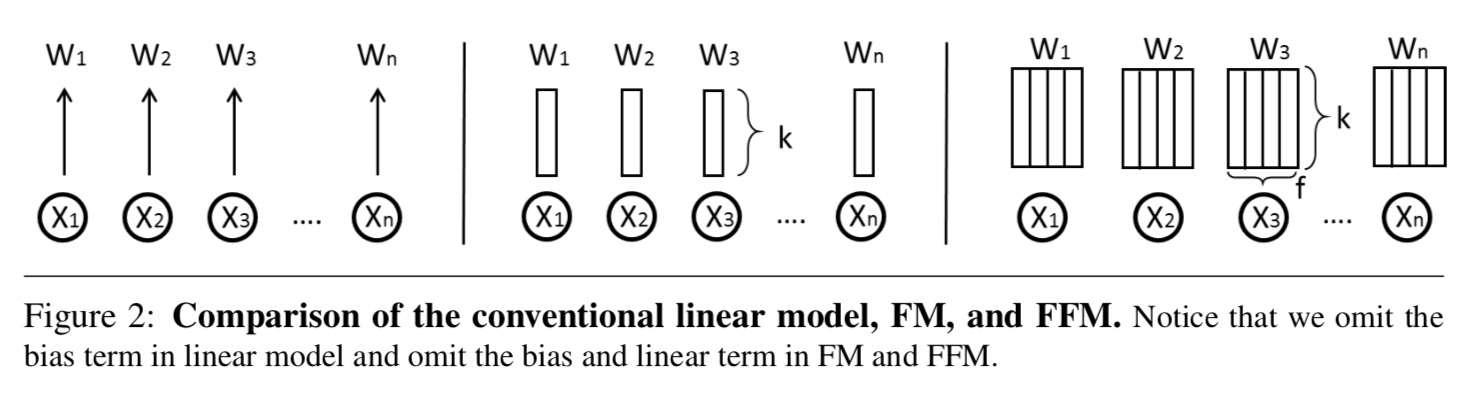
자, 지금까지 CTR 예측에 탁월한 FM, FFM에 대해 알아보았습니다. 모델이 단순하여 numpy로 직접 구현해 보는 것도 그리 어려워 보이지 않습니다. 하지만 여러 open source들이 존재하여 굳이 그럴 필요까지는 없어 보입니다. 필자의 경우에는 xlearn 이라는 python package를 주로 사용합니다. 물론 Dable의 경우 더욱 멋진 알고리듬을 사용하고 있습니다. (BK!)
다음 시간에는 여러 다른 CTR 예측 모델에 대해 추가적으로 다루기로 하겠습니다. 그럼 이만 포스팅을 마치도록 하겠습니다~
감사합니다, Jung-Yup Lee