Bid Shading이란?

1. 서론

안녕하세요, AI팀 안준형입니다. 오늘은 저희 팀에서 최근에 많은 시간과 노력을 들인 입찰 쉐이딩(Bid Shading)에 대해서 소개하려합니다.

2. 입찰 쉐이딩(Bid shading)이란?

온라인 광고에서 직접 판매되지 않는 재고는 주로 실시간 입찰(RTB)에서 프로그램적으로 경매됩니다. 2018년 이전까지 RTB에서는 2등 가격 경매(Second-price Auction, SPA)가 주로 사용되었으며, 여기서 낙찰자는 두 번째로 높은 입찰 가격만 지불하면 되었습니다. 그러나 2017년부터 AppNexus, Index Exchange, OpenX, Rubicon Project, Pubmatic을 포함한 주요 교환소 및 판매측 플랫폼(SSP)들은 1등 가격 경매(First-price Auction, FPA)를 도입하거나 테스트하기 시작했습니다. Google AdX는 2019년에 FPA로 전환했습니다. SPA에서 FPA로의 전환에는 몇 가지 이유가 있었습니다. 첫째, FPA는 입찰자가 정확히 자신이 제시한 가격을 지불하기 때문에 입찰자에게 더 큰 투명성과 책임을 제공했습니다. 둘째, 수정되지 않은 SPA는 헤더 비딩(Header Bidding)의 널리 퍼진 관행과 호환되지 않는 것으로 나타났습니다.

수요측 플랫폼(Demand-side Platform)에게 있어, SPA에서 FPA로의 전환은 입찰 전략을 크게 조정해야 한다는 것을 의미했습니다. SPA에서는 경매 이론에 따라 입찰자가 실제 가치를 입찰하는 것이 지배 전략이었습니다. 즉, DSP가 경매되는 재고의 가치를 계산하고 이 가치를 입찰 가격으로 제출하는 것이 최적의 전략이었습니다. 그러나 FPA에서는 이러한 전략이 DSP가 과도하게 입찰하여 손해를 보는 결과를 초래할 수 있습니다. 이는 SPA와 FPA 간의 근본적인 지불 방식의 차이에서 비롯됩니다. FPA에서는 DSP가 다른 입찰자의 행동, 즉 다른 입찰자의 입찰 가격을 추정하여 이를 자신의 입찰 전략에 반영해야 손해액을 최소화할 수 있습니다.

따라서 DSP는 최적의 입찰 가격을 찾기 위해 최소 승리 가격을 최대한 정확하게 추정하고, 이를 기반으로 원래의 입찰 가격을 조정해야 합니다. 이 과정을 입찰 쉐이딩(Bid Shading)이라고 합니다. 입찰 쉐이딩에서는 입찰자가 경쟁자들이 제시할 가능성이 높은 최고 입찰가를 추정하고, 이보다 약간 높은 입찰가를 제출합니다. 이를 통해 입찰자는 실제 가치보다 낮은 가격으로 경매에서 승리하여, 입찰가와 실제 가치의 차이인 잉여(입찰 전 가격 - 최종 입찰 가격)를 최대화할 수 있습니다. 입찰 쉐이딩은 온라인 광고에서는 비교적 새로운 개념이지만, 다른 산업의 경매에서는 이미 사용되고 있습니다.

입찰 쉐이딩의 가장 중요한 부분은 입찰 성공률(Bid-win Ratio)과 투자 수익률(ROI) 간의 균형입니다. 입찰 가격을 더 많이 쉐이딩할수록, 즉 최종 입찰 가격이 낮아질수록, 입찰이 성공할 경우 ROI가 향상됩니다. 그러나 낮은 입찰 가격은 입찰 성공 확률을 낮추기도 합니다. 그렇기 때문에, 입찰 성공을 할 수 있는 선에서 최대한 가격을 많이 깎는 알고리즘 개발이 필수입니다.

3. 어떻게 가격을 쉐이딩할까?

“An Efficient Deep Distribution Network for Bid Shading in First-Price Auctions” (KDD’ 21)에서는 입찰 성공 확률을 유지하면서 최소 승리 가격을 예측하는 방법론을 제시합니다. 이 방법론은 두 단계로 이루어져있습니다: 1) 분포 추정, 2) 잉여 극대화. 자세한 설명에 들어가기 앞서, 밑에 사용될 수학 기호들에 대해서 간단히 설명하겠습니다.

입찰 쉐이딩의 정량적 목표는 잉여를 최대화하는 것이며, 이때 잉여는 수학적으로 아래와 같이 정의됩니다:

\[S(b; V, \hat{b}) = (V-b)I(b > \hat{b}) = \begin{cases} V-b, &\;\;\text{if}\;\; b > \hat{b}, \\ 0, &\;\;\text{otherwise.}\end{cases}\]

단계 1. 분포 추정 (Distribution Matching)

먼저, 분포 추정 단계에서는 최소 승리 가격(경쟁 입찰가 중 가장 높은 값)의 분포를 학습합니다. 이를 위해 입찰 요청에 대한 입력 특징 벡터(예: 서비스, 인벤토리, 요일, 시간 등)를 기반으로 최소 승리 가격의 조건부 분포를 추정하는 머신러닝 모델을 구축합니다. 이 분포는 확률 밀도 함수(Probability Density Function, PDF)나 누적 분포 함수(Cumulative Density Function, CDF) 형태로 모델링합니다. 분포는 널리 사용되는 normal, exponential, gamma, 혹은 log-normal을 사용합니다. 즉, “아 우리 시스템의 최소 승리 가격의 분포는 normal 분포를 따를거야”라고 가정을 한 후, 이 분포의 파라미터를 학습합니다. 좀 더 생각해보면, 이 가정은 매우 강력하

분포 추정은 최소 승리 가격이 제공되는 경우와 제공되지 않는 경우로 나뉩니다.

1) 최소 승리 가격이 제공되는 경우

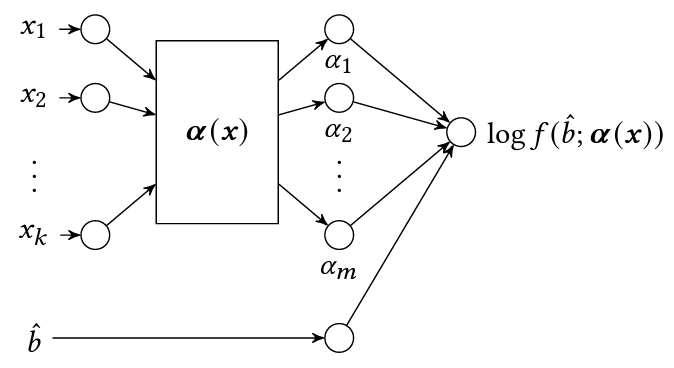
이 경우에는 간단하게, 최소 승리 가격을 맞추는 머신러닝 모델을 학습하면 됩니다. $\{(x^{(i)}, \hat{b}_i)\}_{i=1}^n$ 데이터셋을 통해 PDF, $f(\hat{b}_i; \alpha(x^{(i)}))$를 최대 가능도 추정법(MLE)을 사용하여 학습합니다:

\[\max_{\alpha, \;\hat{b}|x \in \mathcal{D}} \sum_{i=1}^{n} \log f\left( \hat{b}_i; \alpha(x^{(i)}) \right)\]

2) 최소 승리 가격이 제공되지 않는 경우

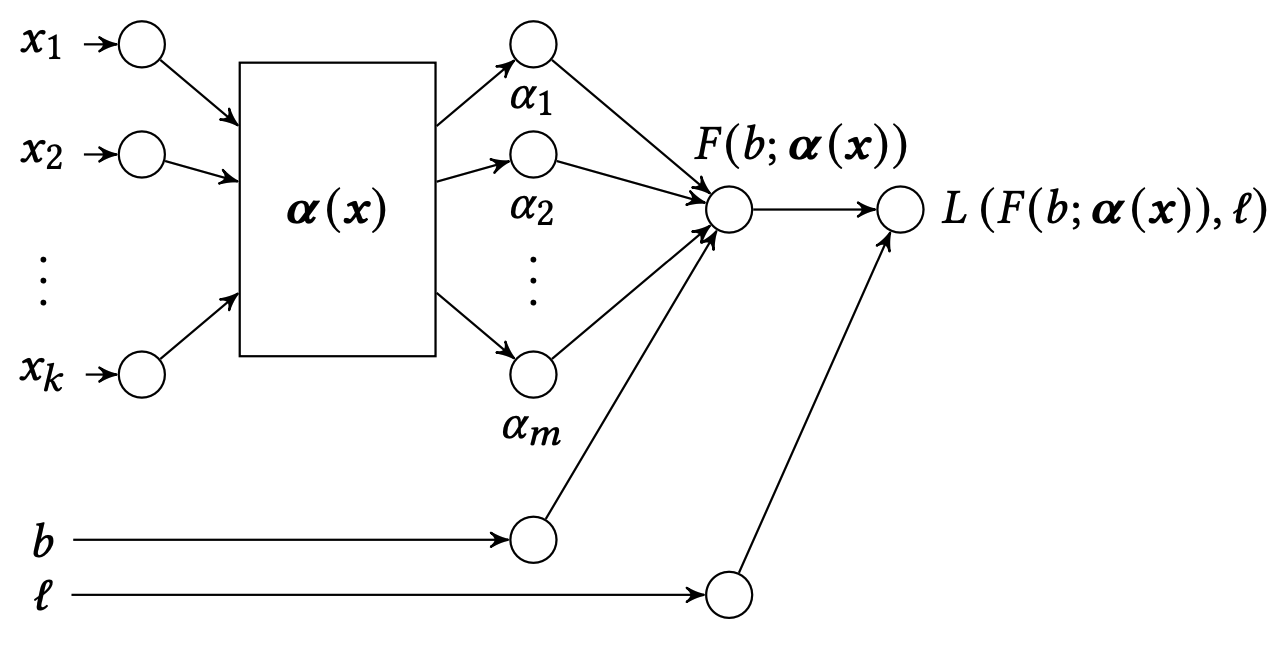
만약 SSP에서 최소 승리 가격을 제공하지 않는 경우 위의 방식은 동작하지 않을 것이며 매우 챌린지한 상황입니다. 이 경우에는 이진 피드백(입찰 성공 여부)을 사용하여 CDF를 추정합니다. 우리가 $\ell_i \in \{0, 1\}$를 입찰 승리 여부라고 정의한다고하면, $\{(x^{(i)}, b_i, \ell_i)\}_{i=1}^n$로 데이터셋을 먼저 구축하고 이걸로 CDF인 $\Pr (\hat{b}_i < b; \alpha(x^{(i)})$을 학습합니다.

\[\max_{\alpha, \;\hat{b}|x \in \mathcal{D}} \sum_{i=1}^{n} L\left( F\left( \hat{b}_i; \alpha(x^{(i)}) \right), \ell_i \right)\]

여기서, $L$은 binary cross entropy을 사용합니다.

단계 2. 잉여 극대화 (Surplus Maximization)

두 번째 단계인 잉여 극대화에서는 위에서 추정된 분포를 기반으로 기대 잉여를 최대화하는 최적의 입찰 가격을 찾습니다. 우리가 기대 잉여 함수를 아래와 같이 표현할 수 있습니다:

\[s(b; V, x) = (V-b)\Pr(\hat{b} < b; \hat{b} \;|\; x )\]

위 수식에서의 확률은 최소 승리 가격이 제공이 되던, 되지 않던 각자만의 방식으로 구할 수 있습니다. 이제 우리가 하고자하는 것은 위의 기대 잉여를 최대화할 수 있는 $b$ 를 찾는 것입니다:

\[\max_{b \in (0, V)} s(b; V, x)\]

이를 위해 제안된 알고리즘은 골든 섹션 검색(Golden Section Search) 알고리즘을 사용하여 수치적으로 안정적인 방법으로 최적의 입찰 가격을 효율적으로 찾습니다. 이 알고리즘은 대부분의 분포에서 유일한 극값(최대 또는 최소값)을 가지며, 실시간 적용에 적합합니다. 알고리즘은 아래와 같습니다.

4. 실험 결과

논문에서는 위의 입찰 쉐이딩 전략을 가지고 오프라인과 온라인 실험을 진행했습니다. 오프라인 데이터셋으로는 논문의 저자들이 속해있는 회사인 Verizon의 데이터를 사용했습니다. 실험 메트릭은 log loss와 surplus로 잡았습니다. Logloss는 낮을수록, surplus는 높을수록 성능이 좋다는 걸 의미합니다.

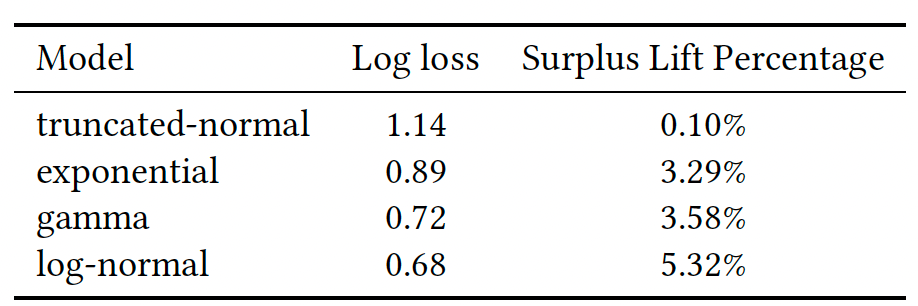
우선, 가정하고 있는 분포를 다양하게 바꿨을 때의 성능은 아래와 같습니다. Log-normal 분포라고 가정하고 이의 파라미터를 학습했을 때 성능이 가장 좋다고 리포트했고, surplus는 무려 9.65% 높게 나왔다고 합니다.

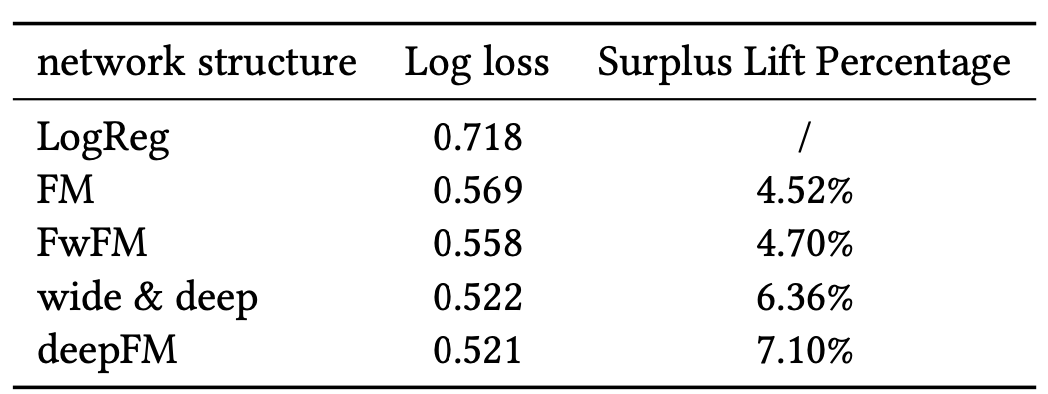
또한, 위 모델 학습 그림에서 $\alpha(x)$로 아무 머신러닝 모델을 사용할 수 있어, 논문에서는 다양한 모델을 사용했다고 합니다. Click-through rate (CTR) 예측 모델로 널리 사용되는 FM, FwFM, Wide & Deep, 그리고 DeepFM을 사용했습니다. 그때, 이 중에서 가장 최신식 모델인 DeepFM이 가장 성능이 좋다고 리포트했습니다. 그냥 로지스틱 회귀를 사용했을 때보다 surplus가 7.1%가량 높은 걸 볼 수 있습니다.

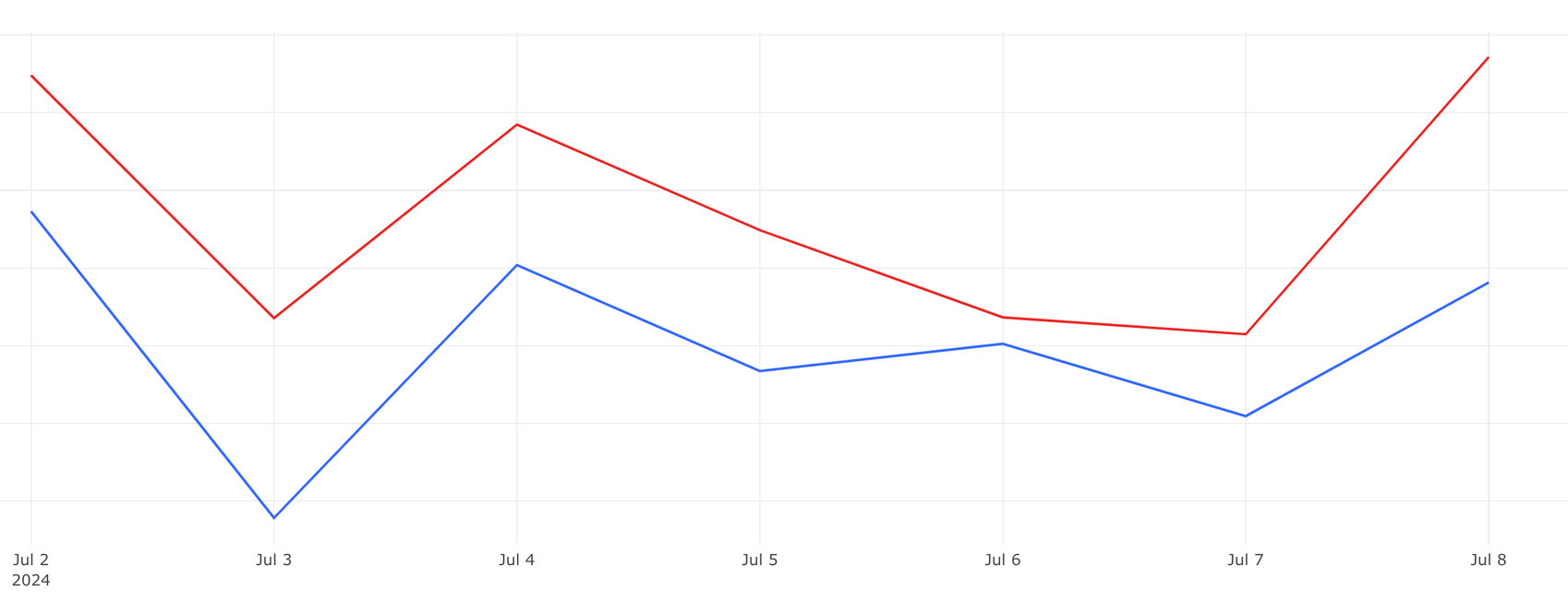
실제 데이블 DSP에 적용했을 때 온라인 성능은 어떻게 되었을까요? 저희는 contribution margin, 즉 순이익을 온라인 메트릭으로 잡았고 결과는 아래 그래프와 같습니다. 입찰 쉐이딩을 적용한 모델이 빨간색 선이고 적용하지 않은 모델이 파란색입니다. 순이익이 입찰 쉐이딩을 적용했을 때 평균적으로 30%정도 증가한 걸 저희는 확인할 수 있었습니다.

5. 마치며

본 연구는 FPA 환경에서의 입찰 쉐이딩 전략을 제시하고, 이를 통해 DSP가 입찰 전략을 최적화하여 ROI를 극대화할 수 있는 방법을 탐구했습니다. 입찰 쉐이딩은 최소 승리 가격을 추정하고 이를 기반으로 최적의 입찰 가격을 설정하여 잉여를 최대화하는 전략입니다. 실험 결과, 제안된 방법론은 다양한 분포 가정 하에서 우수한 성능을 보였으며, 특히 log-normal 분포를 사용할 때 가장 높은 잉여를 기록했습니다. 또한, DeepFM 모델을 사용한 경우 가장 높은 성능을 보였습니다. 실제 온라인 실험에서도 입찰 쉐이딩을 적용한 DSP가 평균적으로 30% 이상의 순이익 증가를 보였습니다.

입찰 쉐이딩 방법론과 구현 모두 어렵지 않은 데에 비해 저희가 얻은 이익은 적지 않습니다. 저희는 이 간단한 알고리즘으로 적지 않은 입찰가를 아낄 수 있을 것이라 예상하고 있습니다.

6. 참고 문헌

그림1: https://persona.ly/glossary/real-time-bidding/bid-shading-making-the-most-of-first-price-auctions/
그림2: https://www.researchgate.net/figure/An-Example-of-Bid-Shading_fig1_222400848
논문: https://arxiv.org/abs/2107.06650