Bayes Theorem

안녕하세요. 오태호입니다.

Bayes Theorem은 Statistics를 공부하다 보면 기초적인 내용중에 하나로 언급되는 내용입니다만, 많은 책의 설명이 너무 추상적이거나 너무 복잡하거나 너무 간단하게 되어 있어서 이해가 쉽지 않은 경우가 많이 있습니다. 그래서 배우기는 분명히 배웠지만 실제로 문제 해결에 적용하기 위해서는 어떻게 적용해야 되는지 잘 모르는 사람도 많이 있습니다.

이 글에서는 Bayes Theorem을 조금 자세히 설명해서 Bayes Theorem의 이해를 돕고, 실제로 문제를 해결하기 위해 Bayes Theorem을 어떤 식으로 적용할 수 있는지 살펴보도록 하겠습니다.

이 글을 이해하기 위해서는 Statistics에 대한 기초지식이 필요합니다.

이 글에서는 Probability Mass Function은 \(P\)와 같이 대문자로 표기하고, Probability Density Function은 \(p\)와 같이 소문자로 표기하였습니다.

이 글은 Ubuntu 18.04.2, Python 3.10.11, NumPy 1.24.3, Matplotlib 3.7.1, PyMC 5.4.0, ArviZ 0.15.1을 사용해서 작성했습니다.

Conditional Probability

Bayes Theorem을 이해하기 위해서는 Conditional Probability에 대한 이해가 필요합니다. Conditional Probability의 정의는 다음과 같습니다.

\[P(A \mid B)=\frac{P(A \cap B)}{P(B)}\]

Event \(B\)가 발생했을 때 Event \(A\)가 발생할 확률은 \(P(A \mid B)\) 로 표기합니다. 그리고 이 확률은 Event \(A\)와 Event \(B\)가 둘 다 발생할 확률에서, Event \(B\)가 발생할 확률을 나눠준 값입니다.

예를 들어서 좀 더 구체적으로 살펴보겠습니다.

어떤 사람이 트럼프 카드를 한 장 들고 있는데 하트 모양을 들고 나에게 안 보이게 들고 있다고 해 봅시다. 나에게 그 카드의 모양을 맞춰보라고 했을 때 모양을 맞출 수 있는 확률은 (가능한 모양은 스페이드, 클로버, 다이아몬드, 하트로 총 \(4\)가지가 있으므로) \(\frac{1}{4}\)입니다. 만약에 이 사람이 자신이 들고 있는 카드는 빨간 색이라고 미리 알려준다면 나는 그 카드의 모양을 맞출 수 있는 확률은 (가능한 모양이 다이아몬드, 하트로 총 \(2\)가지가 있으므로) \(\frac{1}{2}\)이 됩니다. 이 상황을 Conditional Probability의 수식에 그대로 적용해서 정리하면 다음과 같습니다.

• \(P(A) =\) 하트 모양을 들고 있을 확률 \(= \frac{1}{4}\)
• \(P(B) =\) 빨간 색을 들고 있을 확률 \(= \frac{1}{2}\)
• \(P(A \cap B) =\) 빨간 색 하트 모양을 들고 있을 확률 \(= \frac{1}{4}\)
• \(P(A \mid B) =\) 들고 있는 색이 빨간 색일 때 하트 모양을 들고 있을 확률 \(= \frac{\frac{1}{4}}{\frac{1}{2}} = \frac{1}{2}\)

참고로 빨간 색 하트 모양을 들고 있을 확률은 (하트 모양은 항상 빨간 색을 가지므로) 하트 모양을 들고 있을 확률과 동일합니다.

Bayes Theorem

앞에서 살펴본 Conditional Probability를 이용해서 정리하면 다음과 같습니다.

\[P(A \mid B)=\frac{P(A \cap B)}{P(B)} \\ P(A \mid B)P(B)=P(A \cap B)\]

\(A\)와 \(B\)를 바꿔서 정리하면 다음과 같습니다.

\[P(B \mid A)=\frac{P(B \cap A)}{P(A)} \\ P(B \mid A)P(A)=P(B \cap A)\]

이 내용을 이용해서 정리하면 다음과 같습니다.

\[P(A \mid B)P(B)=P(A \cap B)=P(B \cap A)=P(B \mid A)P(A) \\ P(A \mid B)P(B)=P(B \mid A)P(A) \\ P(A \mid B)=\frac{P(B \mid A)P(A)}{P(B)}\]

이것이 Bayes Theorem이며 다시 정리하면 다음과 같습니다.

\[P(A \mid B)=\frac{P(B \mid A)P(A)}{P(B)}\]

참고로 여기에서 각각은 다음과 같은 명칭을 가지고 있습니다. 각각에 대해서는 뒤로 가면서 조금씩 자세히 다룰 예정입니다.

• \(P(A) =\) Prior

• \(P(B) =\) Evidence

• \(P(B \mid A) =\) Likelihood

• \(P(A \mid B) =\) Posterior

Conditional Probability에서 살펴봤던 트럼프 카드 예시를 다시 살펴보면 다음과 같습니다.

• \(P(A) =\) 하트 모양을 들고 있을 확률 \(= \frac{1}{4}\)

• \(P(B) =\) 빨간 색을 들고 있을 확률 \(= \frac{1}{2}\)

• \(P(B \mid A) =\) 들고 있는 모양이 하트 모양일 때 빨간 색일 확률 \(= 1\)

• \(P(A \mid B) =\) 들고 있는 색이 빨간 색일 때 하트 모양을 들고 있을 확률 \(= \frac{1 \times \frac{1}{4}}{\frac{1}{2}} = \frac{1}{2}\)

Coin Toss - Discrete Probability

동전 던지기를 통해서 Bayes Theorem을 좀 더 자세히 살펴보겠습니다.

앞면이 나올 확률이 \(\frac{1}{4}\), \(\frac{1}{2}\), \(\frac{3}{4}\) 중에 하나인 동전이 하나 있습니다만, 이 동전의 앞면이 나올 확률이 얼마인지 모릅니다. 이 동전을 한 번 던져 보았는데 앞면이 나왔습니다. 이 동전의 앞면이 나올 확률이 얼마인지 추정하고 싶습니다.

헷갈리지 않기 위해 Bayes Theorem의 Notation을 조금 바꿔서 표기해 보겠습니다.

\[P(\theta \mid D=1)=\frac{P(D=1 \mid \theta)P(\theta)}{P(D=1)}\]

동전은 이미 한 번 던졌고 앞면이 이미 나왔기 때문에 앞면이 나왔다는 사실을 \(D=1\)로 표기했습니다. (뒷면은 \(D=0\)으로 표기합니다.) 여기서 자세히 살펴보면 다음과 같은 몇 가지 중요한 사실을 알 수 있습니다.

• \(P(\theta)\)은 \(\theta\)에 대한 Function이며 Probability Mass Function입니다.
  • Probability Mass Function이기 때문에 가능한 모든 경우의 \(\theta\)의 Function 값을 합하면 \(1\)이 됩니다.
  • \[\sum_\theta P(\theta)=1\]
• \(P(\theta \mid D=1)\)은 \(\theta\)에 대한 Function이며 Probability Mass Function입니다.
  • Probability Mass Function이기 때문에 가능한 모든 경우의 \(\theta\)의 Function 값을 합하면 \(1\)이 됩니다.
  • \[\sum_\theta P(\theta \mid D=1)=1\]
• \(P(D=1 \mid \theta)\)은 \(\theta\)에 대한 Function이며 Probability Mass Function이 아닙니다.
  • Probability Mass Function이 아니기 때문에 가능한 모든 경우의 \(\theta\)의 Function 값을 합해도 \(1\)이 되지 않습니다.
  • \[\sum_\theta P(D=1 \mid \theta) \neq 1\]
• \(P(D=1)\)은 Constant입니다.
  • \[P(D=1)=\sum_\theta P(D=1 \mid \theta)P(\theta)\]
    • 증명은 다음과 같습니다. \(P(\theta \mid D=1)=\frac{P(D=1 \mid \theta)P(\theta)}{P(D=1)} \\ \sum_\theta P(\theta \mid D=1)=\sum_\theta \frac{P(D=1 \mid \theta)P(\theta)}{P(D=1)} \\ 1=\sum_\theta \frac{P(D=1 \mid \theta)P(\theta)}{P(D=1)} \\ P(D=1)=\sum_\theta P(D=1 \mid \theta)P(\theta)\)
  • \(\sum_\theta P(\theta \mid D=1)=1\)가 성립하도록 만들기 위한 Normalize Term으로 이해할 수도 있습니다.

다음과 같이 Prior를 정의합니다. Prior는 현재 동전에 대한 정보가 없기 때문에 적당히 정의합니다.

• \(P(\theta = \frac{1}{4}) =\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{4}\)일 확률

  \[= \frac{1}{3}\]

• \(P(\theta = \frac{1}{2}) =\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{2}\)일 확률

  \[= \frac{1}{3}\]

• \(P(\theta = \frac{3}{4}) =\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{3}{4}\)일 확률

  \[= \frac{1}{3}\]

가지고 있는 동전의 앞면이 나올 확률인 \(\theta\)는 \(\frac{1}{4}\), \(\frac{1}{2}\), \(\frac{3}{4}\)중에 하나의 값을 가지고 있다는 사실은 알고 있지만 어느 값을 가지고 있을지는 전혀 모르기 때문에 균등하게 모두 각각이 \(\frac{1}{3}\)의 확률로 가질 수 있다고 정의했습니다. 만약에 \(\theta\)가 \(\frac{1}{2}\)일 확률이 다른 경우보다 더 높다는 사실을 알고 있다면 \(\theta\)가 \(\frac{1}{2}\)인 경우에 조금 더 높은 확률을 가지고 있는 것으로 Prior를 정의할 수도 있습니다.

Likelihood는 다음과 같이 계산합니다.

• \(P(D=1 \mid \theta = \frac{1}{4}) =\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{4}\)일 때, 동전을 던져서 앞면이 나올 확률

  \[= \frac{1}{4}\]

• \(P(D=1 \mid \theta = \frac{1}{2}) =\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{2}\)일 때, 동전을 던져서 앞면이 나올 확률

  \[= \frac{1}{2}\]

• \(P(D=1 \mid \theta = \frac{3}{4}) =\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{3}{4}\)일 때, 동전을 던져서 앞면이 나올 확률

  \[= \frac{3}{4}\]

Likelihood는 Probability Mass Function이 아니기 때문에 가능한 모든 경우의 \(\theta\)의 Function 값을 합해도 \(1\)이 되지 않습니다. (\(\frac{1}{4} + \frac{1}{2} + \frac{3}{4} = \frac{3}{2} \neq 1\))

Evidence는 다음과 같이 계산합니다.

• \(P(D=1)=\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)에 대한 정보가 없을 때, 동전을 던져서 앞면이 나올 확률

  \[=\sum_\theta P(D=1 \mid \theta)P(\theta) \\ =P(D=1 \mid \theta = \frac{1}{4})P(\theta = \frac{1}{4}) \\ +P(D=1 \mid \theta = \frac{1}{2})P(\theta = \frac{1}{2}) \\ +P(D=1 \mid \theta = \frac{3}{4})P(\theta = \frac{3}{4}) \\ =\frac{1}{4}\times\frac{1}{3}+\frac{1}{2}\times\frac{1}{3}+\frac{3}{4}\times\frac{1}{3} \\ =\frac{1}{12}+\frac{1}{6}+\frac{1}{4} \\ =\frac{1}{12}+\frac{2}{12}+\frac{3}{12} \\ =\frac{6}{12} \\ =\frac{1}{2}\]

Posterior는 다음과 같이 계산합니다.

• \(P(\theta=\frac{1}{4} \mid D=1)=\) 동전을 던져서 앞면이 나왔을 때, 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{4}\)일 확률

  \[=\frac{P(D=1 \mid \theta=\frac{1}{4})P(\theta=\frac{1}{4})}{P(D=1)}=\frac{\frac{1}{4}\times\frac{1}{3}}{\frac{1}{2}}=\frac{1}{6}\]

• \(P(\theta=\frac{1}{2} \mid D=1)=\) 동전을 던져서 앞면이 나왔을 때, 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{2}\)일 확률

  \[=\frac{P(D=1 \mid \theta=\frac{1}{2})P(\theta=\frac{1}{2})}{P(D=1)}=\frac{\frac{1}{2}\times\frac{1}{3}}{\frac{1}{2}}=\frac{1}{3}\]

• \(P(\theta=\frac{3}{4} \mid D=1)=\) 동전을 던져서 앞면이 나왔을 때, 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{3}{4}\)일 확률

  \[=\frac{P(D=1 \mid \theta=\frac{3}{4})P(\theta=\frac{3}{4})}{P(D=1)}=\frac{\frac{3}{4}\times\frac{1}{3}}{\frac{1}{2}}=\frac{1}{2}\]

문제를 다시 한 번 살펴보겠습니다.

앞면이 나올 확률이 \(\frac{1}{4}\), \(\frac{1}{2}\), \(\frac{3}{4}\) 중에 하나인 동전이 하나 있습니다만, 이 동전의 앞면이 나올 확률이 얼마인지 모릅니다. 이 동전을 한 번 던져 보았는데 앞면이 나왔습니다. 이 동전의 앞면이 나올 확률이 얼마인지 추정하고 싶습니다.

앞에서 계산한 내용을 바탕으로 정리하면 다음과 같습니다.

• 동전의 앞면이 나올 확률이 \(\frac{1}{4}\)일 확률이 \(\frac{1}{6}\)입니다.

• 동전의 앞면이 나올 확률이 \(\frac{1}{2}\)일 확률이 \(\frac{1}{3}\)입니다.

• 동전의 앞면이 나올 확률이 \(\frac{3}{4}\)일 확률이 \(\frac{1}{2}\)입니다.

직관적으로 생각해 보았을 때 동전을 한 번 던져서 앞면이 나왔기 때문에 동전의 앞면이 나올 확률이 \(\frac{3}{4}\)일 확률이 Prior에서 예측한 \(\frac{1}{3}\)보다 높을 것으로 예상되는데, 예상대로 \(\frac{1}{3}\)보다 높은 \(\frac{1}{2}\)입니다. 한 번 더 나아가 보도록 하겠습니다.

이 상황에서 이 동전을 한 번 더 던져 보았는데 이번에는 뒷면이 나왔습니다. 이 동전의 앞면이 나올 확률이 얼마인지 추정하고 싶습니다.

동전을 한 번도 안 던져서 정보가 없었을 때는 Prior가 다음과 같았습니다.

• \[P(\theta = \frac{1}{4}) = \frac{1}{3}\]
• \[P(\theta = \frac{1}{2}) = \frac{1}{3}\]
• \[P(\theta = \frac{3}{4}) = \frac{1}{3}\]

하지만 지금은 이미 동전을 한 번 던져서 동전에 대한 정보가 Posterior의 형태로 수집되었습니다. 이 수집된 Posterior를 다음과 같이 새로운 Prior로 사용합니다.

• \[P(\theta = \frac{1}{4}) = \frac{1}{6}\]
• \[P(\theta = \frac{1}{2}) = \frac{1}{3}\]
• \[P(\theta = \frac{3}{4}) = \frac{1}{2}\]

Likelihood는 다음과 같이 계산합니다.

• \(P(D=0 \mid \theta = \frac{1}{4}) =\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{4}\)일 때, 동전을 던져서 뒷면이 나올 확률

  \[= \frac{3}{4}\]

• \(P(D=0 \mid \theta = \frac{1}{2}) =\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{2}\)일 때, 동전을 던져서 뒷면이 나올 확률

  \[= \frac{1}{2}\]

• \(P(D=0 \mid \theta = \frac{3}{4}) =\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{3}{4}\)일 때, 동전을 던져서 뒷면이 나올 확률

  \[= \frac{1}{4}\]

Evidence는 다음과 같이 계산합니다.

• \(P(D=0)=\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)에 대한 정보가 없을 때, 동전을 던져서 뒷면이 나올 확률

  \[=\sum_\theta P(D=0 \mid \theta)P(\theta) \\ =P(D=0 \mid \theta = \frac{1}{4})P(\theta = \frac{1}{4}) \\ +P(D=0 \mid \theta = \frac{1}{2})P(\theta = \frac{1}{2}) \\ +P(D=0 \mid \theta = \frac{3}{4})P(\theta = \frac{3}{4}) \\ =\frac{3}{4}\times\frac{1}{6}+\frac{1}{2}\times\frac{1}{3}+\frac{1}{4}\times\frac{1}{2} \\ =\frac{1}{8}+\frac{1}{6}+\frac{1}{8} \\ =\frac{3}{24}+\frac{4}{24}+\frac{3}{24} \\ =\frac{10}{24} \\ =\frac{5}{12}\]

Posterior는 다음과 같이 계산합니다.

• \(P(\theta=\frac{1}{4} \mid D=0)=\) 동전을 던져서 뒷면이 나왔을 때, 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{4}\)일 확률

  \[=\frac{P(D=0 \mid \theta=\frac{1}{4})P(\theta=\frac{1}{4})}{P(D=0)}=\frac{\frac{3}{4}\times\frac{1}{6}}{\frac{5}{12}}=\frac{3}{10}\]

• \(P(\theta=\frac{1}{2} \mid D=0)=\) 동전을 던져서 뒷면이 나왔을 때, 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{1}{2}\)일 확률

  \[=\frac{P(D=0 \mid \theta=\frac{1}{2})P(\theta=\frac{1}{2})}{P(D=0)}=\frac{\frac{1}{2}\times\frac{1}{3}}{\frac{5}{12}}=\frac{2}{5}\]

• \(P(\theta=\frac{3}{4} \mid D=0)=\) 동전을 던져서 뒷면이 나왔을 때, 동전을 던져서 앞면이 나올 확률인 \(\theta\)가 \(\frac{3}{4}\)일 확률

  \[=\frac{P(D=0 \mid \theta=\frac{3}{4})P(\theta=\frac{3}{4})}{P(D=0)}=\frac{\frac{1}{4}\times\frac{1}{2}}{\frac{5}{12}}=\frac{3}{10}\]

문제를 다시 한 번 살펴보겠습니다.

앞면이 나올 확률이 \(\frac{1}{4}\), \(\frac{1}{2}\), \(\frac{3}{4}\) 중에 하나인 동전이 하나 있습니다만, 이 동전의 앞면이 나올 확률이 얼마인지 모릅니다. 이 동전을 한 번 던져 보았는데 앞면이 나왔습니다. 이 동전을 다시 한 번 던져 보았는데 뒷면이 나왔습니다. 이 동전의 앞면이 나올 확률이 얼마인지 추정하고 싶습니다.

앞에서 계산한 내용을 바탕으로 정리하면 다음과 같습니다.

• 동전의 앞면이 나올 확률이 \(\frac{1}{4}\)일 확률이 \(\frac{3}{10}\)입니다.

• 동전의 앞면이 나올 확률이 \(\frac{1}{2}\)일 확률이 \(\frac{2}{5}\)입니다.

• 동전의 앞면이 나올 확률이 \(\frac{3}{4}\)일 확률이 \(\frac{3}{10}\)입니다.

직관적으로 생각해 보았을 때 동전을 한 번 던져서 앞면이 나왔고 또 한 번 던져서 뒷면이 나왔기 때문에 동전의 앞면이 나올 확률이 \(\frac{1}{4}\)나 \(\frac{3}{4}\)인 경우보다 \(\frac{1}{2}\)인 경우의 확률이 높을 것으로 예상되는데, 예상대로 동전의 앞면이 나올 확률이 \(\frac{1}{2}\)인 경우의 확률이 \(\frac{1}{4}\)나 \(\frac{3}{4}\)인 경우보다 높습니다.

계산과정을 살펴보면 느낄 수 있겠지만, Prior를 어떻게 설정하느냐에 따라 결론이 바뀔 수가 있어서 풀이과정에 수학적 엄밀함이 결여되어 있는 것처럼 보일 수 있습니다. 하지만 초반에 정보가 없어서 다소 부정확한 Prior를 가지고 있더라도 Data를 계속 수집해서 Prior를 계속 Update하다 보면 점점 진실과 가까운 결론을 얻게 됩니다.

Coin Toss - Continuous Probability

Coin Toss 문제를 조금 더 일반화해서 살펴보겠습니다.

앞면이 나올 확률을 모르는 동전이 하나 있습니다. 이 동전을 한 번 던져 보았는데 앞면이 나왔습니다. 이 동전의 앞면이 나올 확률이 얼마인지 추정하고 싶습니다.

이전 Coin Toss 문제와 거의 흡사해 보이지만 이전에는 동전의 앞면이 나올 확률이 \(\frac{1}{4}\), \(\frac{1}{2}\), \(\frac{3}{4}\)중에 하나라고 알고 있었지만 이번에는 그런 정보도 없는 상태입니다.

이전 Coin Toss 문제는 \(\theta\)가 Discrete한 값을 가졌지만 여기서는 \(\theta\)가 Continuous한 값을 가지기 때문에 Probability Mass Function대신에 Probability Density Function을 사용해서 다음과 같이 Bayes Theorem을 표현합니다.

\[p(\theta \mid D=1)=\frac{p(D=1 \mid \theta)p(\theta)}{p(D=1)}\]

각 부분은 다음과 같은 특징이 있습니다.

• \(\theta\)는 확률이기 때문에 \(0\)부터 \(1\)의 값을 가집니다.
• \(p(\theta)\)은 \(\theta\)에 대한 Function이며 Probability Density Function입니다.
  • Probability Density Function이기 때문에 가능한 모든 경우의 \(\theta\)의 Function 값을 적분하면 \(1\)이 됩니다.
  • \[\int_0^1p(\theta)d\theta=1\]
• \(p(\theta \mid D=1)\)은 \(\theta\)에 대한 Function이며 Probability Density Function입니다.
  • Probability Density Function이기 때문에 가능한 모든 경우의 \(\theta\)의 Function 값을 적분하면 \(1\)이 됩니다.
  • \[\int_0^1p(\theta \mid D=1)d\theta=1\]
• \(p(D=1 \mid \theta)\)은 \(\theta\)에 대한 Function이며 Probability Density Function이 아닙니다.
  • Probability Density Function이 아니기 때문에 가능한 모든 경우의 \(\theta\)의 Function 값을 적분해도 \(1\)이 되지 않습니다.
  • \[\int_0^1p(D=1 \mid \theta)d\theta \neq 1\]
• \(p(D=1)\)은 Constant입니다.
  • \[p(D=1)=\int_0^1 p(D=1 \mid \theta)p(\theta)d\theta\]
  • \(\int_0^1p(\theta \mid D=1)d\theta=1\)가 성립하도록 만들기 위한 Normalize Term으로 이해할 수도 있습니다.

다음과 같이 Prior를 정의합니다. Prior는 현재 동전에 대한 정보가 없기 때문에 모든 \(\theta\)에 대해 균일하게 정의합니다.

• \[p(\theta)= \begin{cases} 1 & \text{ if } 0 \le \theta \le 1 \\ 0 & \text{ otherwise } \end{cases}\]

Likelihood는 다음과 같이 계산합니다.

• \(p(D=1 \mid \theta) =\) 동전을 던져서 앞면이 나올 확률이 \(\theta\)일 때, 동전을 던져서 앞면이 나올 확률

  \[= \theta\]

Evidence는 다음과 같이 계산합니다.

• \(p(D=1)=\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)에 대한 정보가 없을 때, 동전을 던져서 앞면이 나올 확률

  \[=\int_0^1 p(D=1 \mid \theta)p(\theta)d\theta \\ =\int_0^1 p(D=1 \mid \theta)d\theta \\ =\int_0^1 \theta d\theta \\ =\left [ \frac{1}{2}\theta^2 \right ]_0^1 \\ =\frac{1}{2}\]

Posterior는 다음과 같이 계산합니다.

• \(p(\theta \mid D=1)=\) 동전을 던져서 앞면이 나왔을 때, 동전을 던져서 앞면이 나올 확률인 \(\theta\)의 확률밀도

  \[=\frac{p(D=1 \mid \theta)p(\theta)}{p(D=1)}=\frac{\theta}{\frac{1}{2}}=2\theta\]

직관적으로 생각해 보았을 때 동전을 한 번 던져서 앞면이 나왔기 때문에 동전의 앞면이 나올 확률이 높을 것으로 예상되는데 Posterior를 살펴보면 예상대로 동전의 앞면이 나올 확률인 \(\theta\)의 값이 큰 값을 가질 확률이 높습니다.

한 번 더 나아가 보도록 하겠습니다.

이 상황에서 이 동전을 한 번 더 던져 보았는데 이번에는 뒷면이 나왔습니다. 이 동전의 앞면이 나올 확률이 얼마인지 추정하고 싶습니다.

동전을 한 번도 안 던져서 정보가 없었을 때는 Prior가 다음과 같았습니다.

• \[p(\theta)= \begin{cases} 1 & \text{ if } 0 \le \theta \le 1 \\ 0 & \text{ otherwise } \end{cases}\]

하지만 지금은 이미 동전을 한 번 던져서 동전에 대한 정보가 Posterior의 형태로 수집되었습니다. 이 수집된 Posterior를 다음과 같이 새로운 Prior로 사용합니다.

• \[p(\theta)= \begin{cases} 2\theta & \text{ if } 0 \le \theta \le 1 \\ 0 & \text{ otherwise } \end{cases}\]

Likelihood는 다음과 같이 계산합니다.

• \(p(D=0 \mid \theta) =\) 동전을 던져서 앞면이 나올 확률이 \(\theta\)일 때, 동전을 던져서 뒷면이 나올 확률

  \[= 1 - \theta\]

Evidence는 다음과 같이 계산합니다.

• \(p(D=0)=\) 동전을 던져서 앞면이 나올 확률인 \(\theta\)에 대한 정보가 없을 때, 동전을 던져서 뒷면이 나올 확률

  \[=\int_0^1 p(D=0 \mid \theta)p(\theta)d\theta \\ =\int_0^1 p(D=0 \mid \theta)(2\theta)d\theta \\ =\int_0^1 (1-\theta)(2\theta) d\theta \\ =\int_0^1 (2\theta-2\theta^2) d\theta \\ =\left [ \theta^2 - \frac{2}{3}\theta^3 \right ]_0^1 \\ =1 - \frac{2}{3} \\ =\frac{1}{3}\]

Posterior는 다음과 같이 계산합니다.

• \(p(\theta \mid D=0)=\) 동전을 던져서 뒷면이 나왔을 때, 동전을 던져서 앞면이 나올 확률인 \(\theta\)의 확률밀도

  \[=\frac{p(D=0 \mid \theta)p(\theta)}{p(D=0)}=\frac{(1-\theta)(2\theta)}{\frac{1}{3}}=6\theta(1-\theta)\]

직관적으로 생각해 보았을 때 동전을 한 번 던져서 앞면이 나왔고 또 한 번 던져서 뒷면이 나왔기 때문에 동전의 앞면이 나올 확률이 \(\frac{1}{2}\)일 확률이 가장 높을 것으로 예상되는데, 예상대로 동전의 앞면이 나올 확률이 \(\frac{1}{2}\)인 경우의 확률이 가장 높습니다.

Coin Toss - Numerical Solution

지금까지 다룬 Bayes Theorem의 계산은 매우 간단해서 Analytical Method로 쉽게 계산할 수 있었습니다만, 실제로 문제를 풀다 보면 너무 복잡해서 Analytical Method로 계산이 거의 불가능한 경우가 많습니다. 이런 경우에는 Computer의 힘을 빌려서 Numerical Method로 계산할 수 있습니다.

여기서는 다음과 같은 문제를 Python을 사용해서 Numerical Method로 계산해 보겠습니다. 이 문제는 Analytical Method로도 쉽게 풀 수 있지만 Numerical Method를 살펴보기 위해 Numerical Method를 사용해서 풀어보겠습니다.

앞면이 나올 확률을 모르는 동전이 하나 있습니다. 이 동전을 열 번 던져서 앞면, 뒷면, 앞면, 앞면, 뒷면, 뒷면, 뒷면, 뒷면, 앞면, 뒷면이 나왔습니다. 이 동전의 앞면이 나올 확률이 얼마인지 추정하고 싶습니다.

from collections import defaultdict
import matplotlib.pyplot as plt

num_digits = 2
num_steps = 100

def new_uniform_pdf():
  pdf = defaultdict(float)
  for i in range(num_steps):
    pdf[round(i / num_steps, num_digits)] = 1.0
  return pdf

def prior(pdf, theta):
  return pdf[round(theta, num_digits)]

def likelihood(x, theta):
  if x == 0:
    return 1 - theta
  else:
    return theta

def normalize(pdf):
  s = sum(pdf.values()) / num_steps
  for k in pdf:
    pdf[k] /= s

def posterior(prior_pdf, x):
  posterior_pdf = defaultdict(float)
  for i in range(num_steps):
    theta = round(i / num_steps, num_digits)
    posterior_pdf[theta] = likelihood(x, theta) * prior(prior_pdf, theta)
  normalize(posterior_pdf)
  return posterior_pdf

def ax_plot(ax, pdf):
  pdf = dict(sorted(pdf.items()))
  ax.plot(pdf.keys(), pdf.values())

data = [1, 0, 1, 1, 0, 0, 0, 0, 1, 0]
fig, axs = plt.subplots(len(data), sharex=True, sharey=True)
pdf = new_uniform_pdf()
for i, x in enumerate(data):
  pdf = posterior(pdf, x)
  ax_plot(axs[i], pdf)
fig.savefig('bayes01.png', dpi=200)

처음에는 Prior를 Uniform Distribution으로 설정하고 Prior에 존재하는 모든 경우의 \(\theta\)를 하나하나 넣어서 모든 \(\theta\)에 대한 Posterior를 계산합니다. 이때 \(\theta\)는 Continuous해서 하나하나 계산이 불가능하기 때문에 \(0.01\)단위로 근사해서 계산합니다. Data를 한 개 넣고, Posterior를 계산하고, 계산한 Posterior를 Prior로 설정하고, 다시 다음 Data를 한 개 넣고, Posterior를 계산하는 과정을 Data를 모두 소진할 때까지 반복합니다. Posterior를 계산할 때는 중간중간에 Evidence로 나눠주는 과정이 필요한데, 이것은 Posterior가 Probability Density Function이기 때문에 \(\theta\)에 대해 적분했을 때 \(1\)이 되어야 된다는 성질을 이용해서 Posterior를 Normalize해서(Posterior를 전체 범위의 \(\theta\)로 적분한 값으로 나눠줘서) 계산합니다.

이것을 실행해서 Posterior의 변화과정을 그려보면 보면 다음과 같습니다.

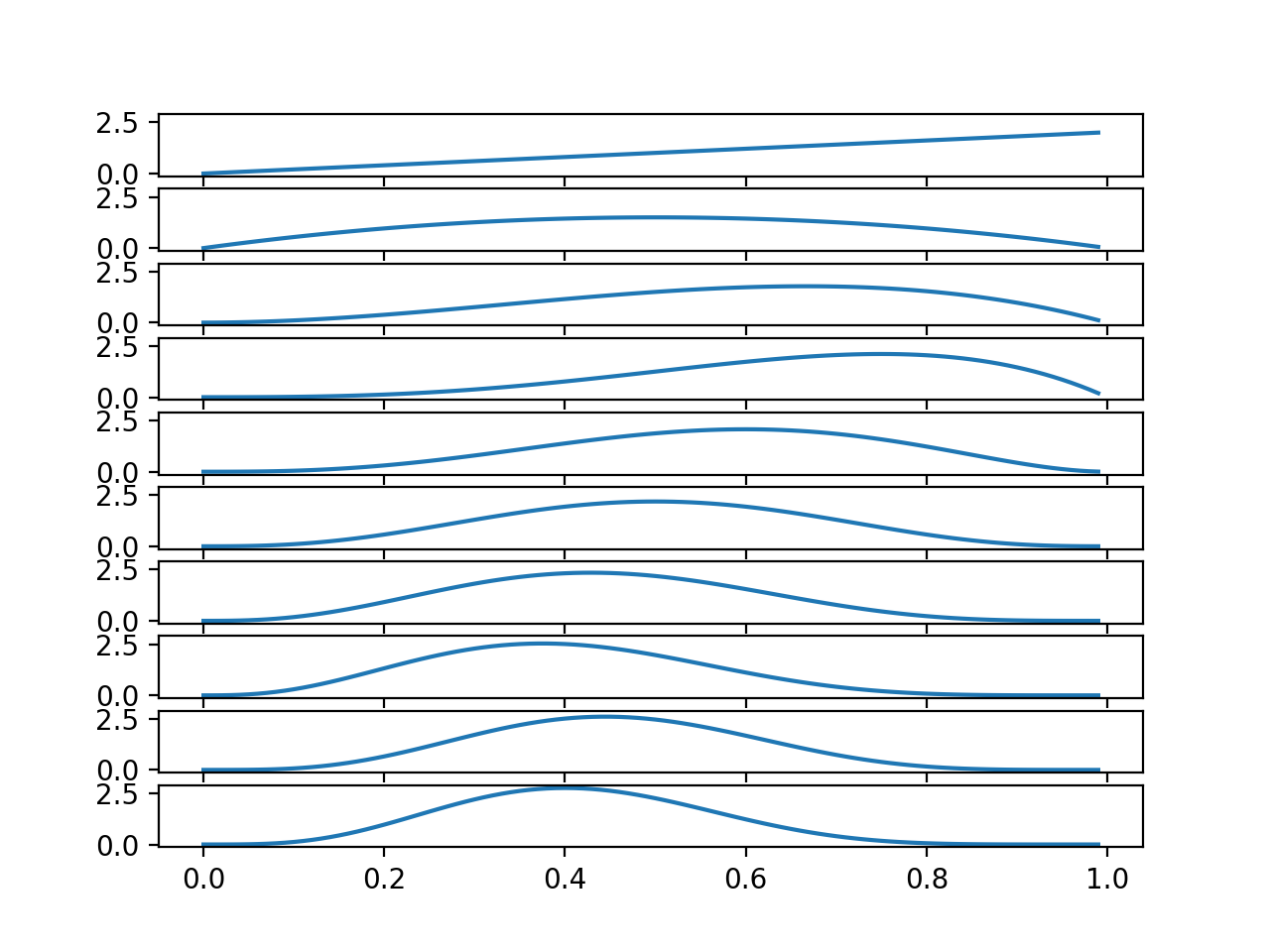
Coin Toss - Continuous Probability에서 동전을 첫 번째 던졌을 때 앞면이 나왔을 때의 Posterior가 \(2\theta\)였고 두 번째 던졌을 때 뒷면이 나왔을 때의 Posterior가 \(6\theta(1-\theta)\)였는데 여기에서 위에서 첫 번째 있는 Graph와 두 번째 있는 Graph를 살펴보면 각각이 예상대로 \(2\theta\), \(6\theta(1-\theta)\)입니다.

동전을 10번 던져서 4번 앞면이 나왔기 때문에, 직관적으로 생각해 보면 \(\theta\)는 \(0.4\)일 확률이 가장 높을 것 같다고 생각되는데, 가장 마지막에 있는 Graph를 살펴보면, 예상대로 \(\theta\)가 \(0.4\)일 확률이 가장 높습니다.

참고로 여기서 Posterior의 변화 추이를 보면서 느낀 분도 있었겠지만 이 Distribution은 Beta Distribution과 동일합니다. \(a\)에 동전 앞면이 나온 횟수 \(+1\)을 설정하고 \(b\)에 동전 뒷면이 나온 횟수 \(+1\)을 설정한 후에 Beta Distribution의 Probability Density Function을 그려보면 확인할 수 있습니다.

Coin Toss - Combined Update

Coin Toss - Numerical Solution에서는 Posterior를 계산할 때 Data를 한 개씩 넣어서 계산했는데, 여러 개를 한꺼번에 넣어서 계산할 수도 있습니다. 여기서는 같은 문제를 푸는데 Data를 다섯 개씩 넣어서 계산해 보도록 하겠습니다.

from collections import defaultdict
import matplotlib.pyplot as plt

num_digits = 2
num_steps = 100

def new_uniform_pdf():
  pdf = defaultdict(float)
  for i in range(num_steps):
    pdf[round(i / num_steps, num_digits)] = 1.0
  return pdf

def prior(pdf, theta):
  return pdf[round(theta, num_digits)]

def likelihood(x, theta):
  p = 1
  for i in x:
    if i == 0:
      p *= (1 - theta)
    else:
      p *= theta
  return p

def normalize(pdf):
  s = sum(pdf.values()) / num_steps
  for k in pdf:
    pdf[k] /= s

def posterior(prior_pdf, x):
  posterior_pdf = defaultdict(float)
  for i in range(num_steps):
    theta = round(i / num_steps, num_digits)
    posterior_pdf[theta] = likelihood(x, theta) * prior(prior_pdf, theta)
  normalize(posterior_pdf)
  return posterior_pdf

def ax_plot(ax, pdf):
  pdf = dict(sorted(pdf.items()))
  ax.plot(pdf.keys(), pdf.values())

data = [[1, 0, 1, 1, 0], [0, 0, 0, 1, 0]]
fig, axs = plt.subplots(len(data), sharex=True, sharey=True)
pdf = new_uniform_pdf()
for i, x in enumerate(data):
  pdf = posterior(pdf, x)
  ax_plot(axs[i], pdf)
fig.savefig('bayes02.png', dpi=200)

달라진 부분을 살펴보도록 하겠습니다. 예전에는 Data를 1개씩 넣으면서 Posterior를 계산하는 방식이었지만, 이번에는 Data를 5개씩 넣으면서 Posterior를 계산하는 방식으로 변경되었습니다. Likelihood는 예전에는 \(\theta\)가 \(0.4\)일 때 동전의 앞면이 나올 확률이 얼마인지를 계산하는 방식으로 되어 있었지만 이번에는 \(\theta\)가 \(0.4\)일 때 동전이 앞면, 뒷면, 앞면, 앞면, 뒷면이 나올 확률이 얼마인지 계산하는 방식으로 변경되었습니다.

이것을 실행해서 Posterior의 변화과정을 그려보면 보면 다음과 같습니다.

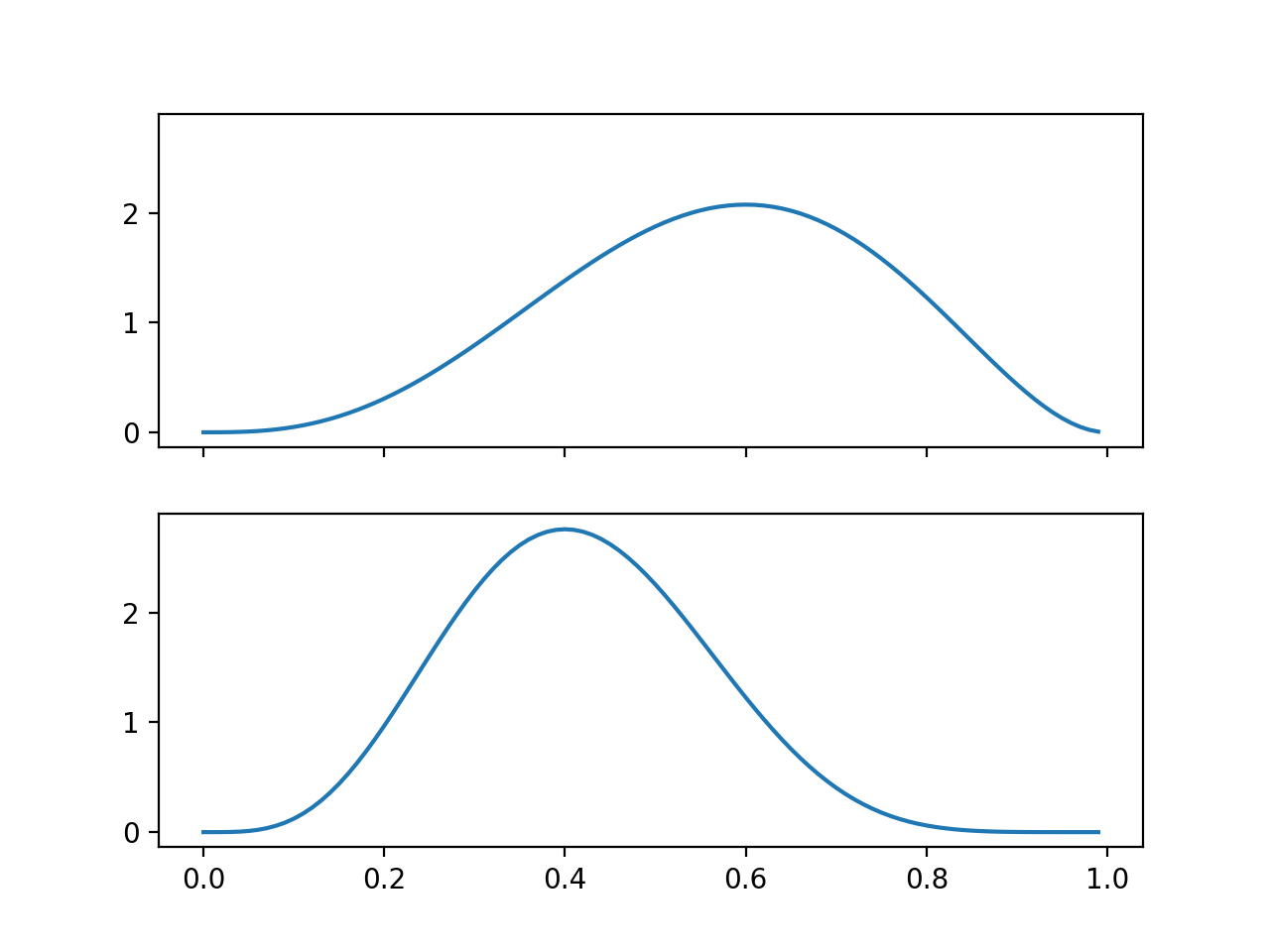
동전을 다섯 번 던졌을 때는 \(\theta\)가 \(0.6\)일 가능성이 높았지만 동전을 다섯 번 더 던졌을 때는 \(\theta\)가 \(0.4\)일 가능성이 높습니다. 이것은 Coin Toss - Numerical Solution에서 다섯 번째와 열 번째 Graph를 살펴보면 결과가 동일합니다.

Coin Toss - Additional Feature

여기서는 조금 복잡한 문제를 풀어보겠습니다.

두 개의 동전이 있습니다. 한 개는 검은색이고 다른 한 개는 흰색입니다. 각각의 동전을 여러 번 던져서 각 동전의 앞면이 나올 확률을 예측하고 싶습니다. 동전을 열 번 던져서 다음과 같은 결과를 얻었습니다.

(앞면, 흰색), (뒷면, 검은색), (앞면, 검은색), (앞면, 흰색), (뒷면, 흰색), (뒷면, 흰색), (뒷면, 흰색), (뒷면, 검은색), (앞면, 검은색), (뒷면, 흰색)

흰색 동전을 던져서 앞면이 나온 경우에 검은색 동전과 흰 색 동전의 앞면이 나올 확률을 계산한다면 다음과 같습니다.

\[p(\theta_b, \theta_w \mid D_1=1, D_2=1)=\frac{p(D_1=1, D_2=1 \mid \theta_b, \theta_w)p(\theta_b, \theta_w)}{p(D_1=1, D_2=1)}\]

• \(D_1\)은 동전이 뒷면인 경우에 \(0\)이고 동전이 앞면인 경우에는 \(1\)입니다.
• \(D_2\)는 동전이 검은색인 경우에 \(0\)이고 동전이 흰색인 경우에 \(1\)입니다.
• \(\theta_b\)는 검은색 동전을 던졌을 때 앞면이 나올 확률입니다.
• \(\theta_w\)는 흰색 동전을 던졌을 때 앞면이 나올 확률입니다.

이렇게 계산하는 것도 가능하지만, 두 동전이 비슷하게 생겼고, 두 동전은 비슷한 성질을 가지고 있을 것으로 예상된다면, 두 동전의 Data를 모두 가지고 각각의 동전의 앞면이 나올 확률을 예측하고 싶을 수도 있습니다. 어느 한 동전의 Data가 부족한 경우에도 다른 동전의 Data를 활용해서 어느정도 예측할 수도 있습니다.

만약에 이렇게 Data를 조금 더 효율적으로 활용하고 싶다면 풀이방법을 다음과 같이 변형할 수 있습니다.

\[p(\theta_1, \theta_2 \mid D_1=1, D_2=1)=\frac{p(D_1=1, D_2=1 \mid \theta_1, \theta_2)p(\theta_1, \theta_2)}{p(D_1=1, D_2=1)}\]

• \[\theta_b=sigmoid(\theta_1)\]
• \[\theta_w=sigmoid(\theta_1+\theta_2)\]
• \[sigmoid(x)=\frac{1}{1+e^{-x}}\]

이렇게 정한 이유는, 검은색 동전은 \(\theta_1\)에 의해 앞면이 나올 확률이 결정되고, 흰색 동전은 검은색 동전과 앞면이 나올 확률이 비슷하지만 \(\theta_2\)만큼의 요소가 추가되어서 앞면이 나올 확률이 결정될 것으로 추정되기 때문입니다. \(sigmoid\)를 사용한 이유는 \(\theta_1\)과 \(\theta_2\)를 사용해서 계산하면 \(0\)보다 작은 숫자가 나오거나 \(1\)보다 큰 숫자가 나올 수가 있어서 결과 범위를 \(0\)부터 \(1\)사이로 변환해 주기 위해서입니다.

이 내용을 바탕으로 Likelihood는 다음과 같이 구성합니다.

• \[p(D_1=0, D_2=0 \mid \theta_1, \theta_2) = 1 - \theta_b = 1 - sigmoid(\theta_1)\]
• \[p(D_1=1, D_2=0 \mid \theta_1, \theta_2) = \theta_b = sigmoid(\theta_1)\]
• \[p(D_1=0, D_2=1 \mid \theta_1, \theta_2) = 1 - \theta_w = 1 - sigmoid(\theta_1 + \theta_2)\]
• \[p(D_1=1, D_2=1 \mid \theta_1, \theta_2) = \theta_w = sigmoid(\theta_1 + \theta_2)\]

import math
from collections import defaultdict
import matplotlib.pyplot as plt

min_p = 0
max_p = 0.4
min_theta = -10
max_theta = 10
num_digits = 1
num_steps = 200

def new_uniform_pdf():
  pdf = defaultdict(float)
  for i in range(num_steps):
    for j in range(num_steps):
      pdf[
          round(
              min_theta + i / num_steps * (max_theta - min_theta), num_digits),
          round(
              min_theta + j / num_steps * (max_theta - min_theta), num_digits)
      ] = 1 / (max_theta - min_theta) ** 2
  return pdf

def prior(pdf, theta1, theta2):
  return pdf[round(theta1, num_digits), round(theta2, num_digits)]

def sigmoid(x):
  return 1 / (1 + math.exp(-x))

def likelihood(x1, x2, theta1, theta2):
  p = 1
  for i1, i2 in zip(x1, x2):
    t = sigmoid(theta1 + theta2 * i2)
    if i1 == 0:
      p *= (1 - t)
    else:
      p *= t
  return p

def normalize(pdf, dim):
  s = sum(pdf.values()) * (((max_theta - min_theta) / num_steps) ** dim)
  for k in pdf:
    pdf[k] /= s

def posterior(prior_pdf, x1, x2):
  posterior_pdf = defaultdict(float)
  theta1_posterior_pdf = defaultdict(float)
  theta2_posterior_pdf = defaultdict(float)
  for i in range(num_steps):
    for j in range(num_steps):
      theta1 = round(
          min_theta + i / num_steps * (max_theta - min_theta), num_digits)
      theta2 = round(
          min_theta + j / num_steps * (max_theta - min_theta), num_digits)
      posterior_pdf[theta1, theta2] = \
          likelihood(x1, x2, theta1, theta2) * prior(prior_pdf, theta1, theta2)
      theta1_posterior_pdf[theta1] += posterior_pdf[(theta1, theta2)]
      theta2_posterior_pdf[theta2] += posterior_pdf[(theta1, theta2)]
  normalize(posterior_pdf, 2)
  normalize(theta1_posterior_pdf, 1)
  normalize(theta2_posterior_pdf, 1)
  return posterior_pdf, theta1_posterior_pdf, theta2_posterior_pdf

def ax_plot(ax, fig, pdf, label):
  pdf = dict(sorted(pdf.items()))
  ax.plot(pdf.keys(), pdf.values())
  ax.set_xlim([min_theta, max_theta])
  ax.set_ylim([min_p, max_p])
  ax.set_xlabel(label)

def ax_tricontour(ax, fig, pdf, label, label2):
  tricontour = ax.tricontour(*zip(*pdf), list(pdf.values()), levels=100,
      vmin=0.0, vmax=0.15, cmap='jet')
  ax.set_xlim([min_theta, max_theta])
  ax.set_ylim([min_theta, max_theta])
  ax.set_xlabel(label)
  ax.set_ylabel(label2)
  fig.colorbar(tricontour, ax=ax)

data1 = [[1, 0, 1, 1, 0], [0, 0, 0, 1, 0]]
data2 = [[1, 0, 0, 1, 1], [1, 1, 0, 0, 1]]
fig1, axs1 = plt.subplots(len(data1), sharex=True, sharey=True)
fig2, axs2 = plt.subplots(len(data1), 2, sharex=True, sharey=True)
pdf = new_uniform_pdf()
for i, (x1, x2) in enumerate(zip(data1, data2)):
  pdf, theta1_pdf, theta2_pdf = posterior(pdf, x1, x2)
  tricontour = ax_tricontour(axs1[i], fig1, pdf, 'theta1', 'theta2')
  ax_plot(axs2[i, 0], fig2, theta1_pdf, 'theta1')
  ax_plot(axs2[i, 1], fig2, theta2_pdf, 'theta2')
fig1.savefig('bayes03_1.png', dpi=200)
fig2.savefig('bayes03_2.png', dpi=200)

fig3, axs3 = plt.subplots(1, 2, sharex=True, sharey=True)
theta_b = defaultdict(float)
theta_w = defaultdict(float)
for i in range(num_steps):
  for j in range(num_steps):
    theta1 = round(
        min_theta + i / num_steps * (max_theta - min_theta), num_digits)
    theta2 = round(
        min_theta + j / num_steps * (max_theta - min_theta), num_digits)
    theta_b[round(sigmoid(theta1), 3)] += prior(pdf, theta1, theta2)
    theta_w[round(sigmoid(theta1 + theta2), 3)] += prior(pdf, theta1, theta2)
theta_b = dict(sorted(theta_b.items()))
axs3[0].plot(theta_b.keys(), theta_b.values())
axs3[0].set_xlabel('theta_b')
theta_w = dict(sorted(theta_w.items()))
axs3[1].plot(theta_w.keys(), theta_w.values())
axs3[1].set_xlabel('theta_w')
fig3.savefig('bayes03_3.png', dpi=200)

\(\theta_1\)과 \(\theta_2\)를 작은 단위로 하나하나 모든 조합에 대해서 Posterior를 계산합니다. \(\theta_1\)과 \(\theta_2\)는 범위가 \(-\infty\)부터 \(\infty\)이기 때문에 적당히 범위를 정해서 \(-10\)부터 \(10\)까지의 범위에서 계산합니다. 여기서는 Data를 5개씩 넣으면서 Posterior를 계산합니다.

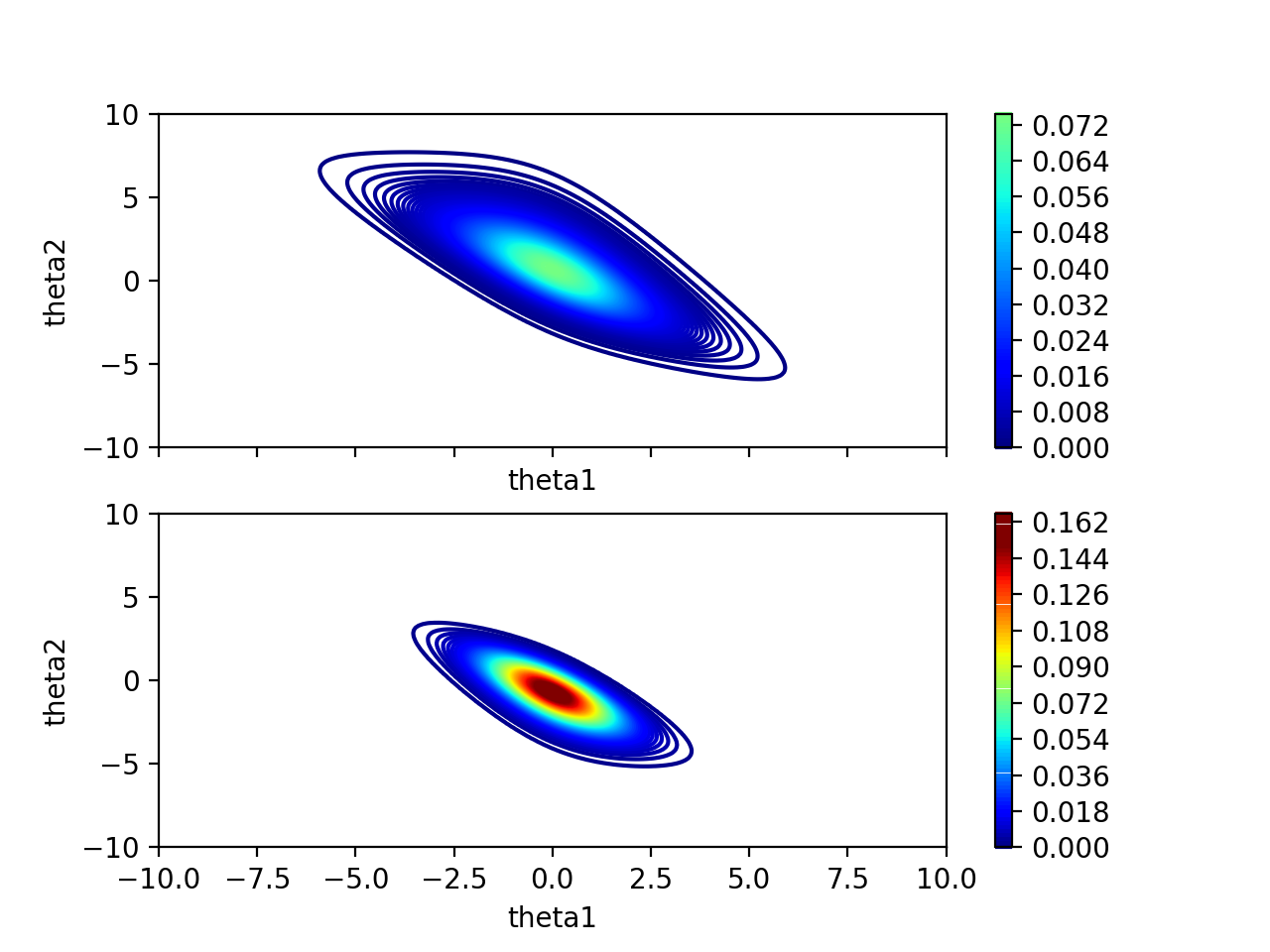
Contour Map을 살펴보면 Data를 넣을수록 점점 \(\theta_1\)과 \(\theta_2\)의 값에 대한 확률이 높아지면서 확신이 생기고 있습니다. \(\theta_1\)과 \(\theta_2\)는 음의 상관관계가 있는 것도 보입니다.

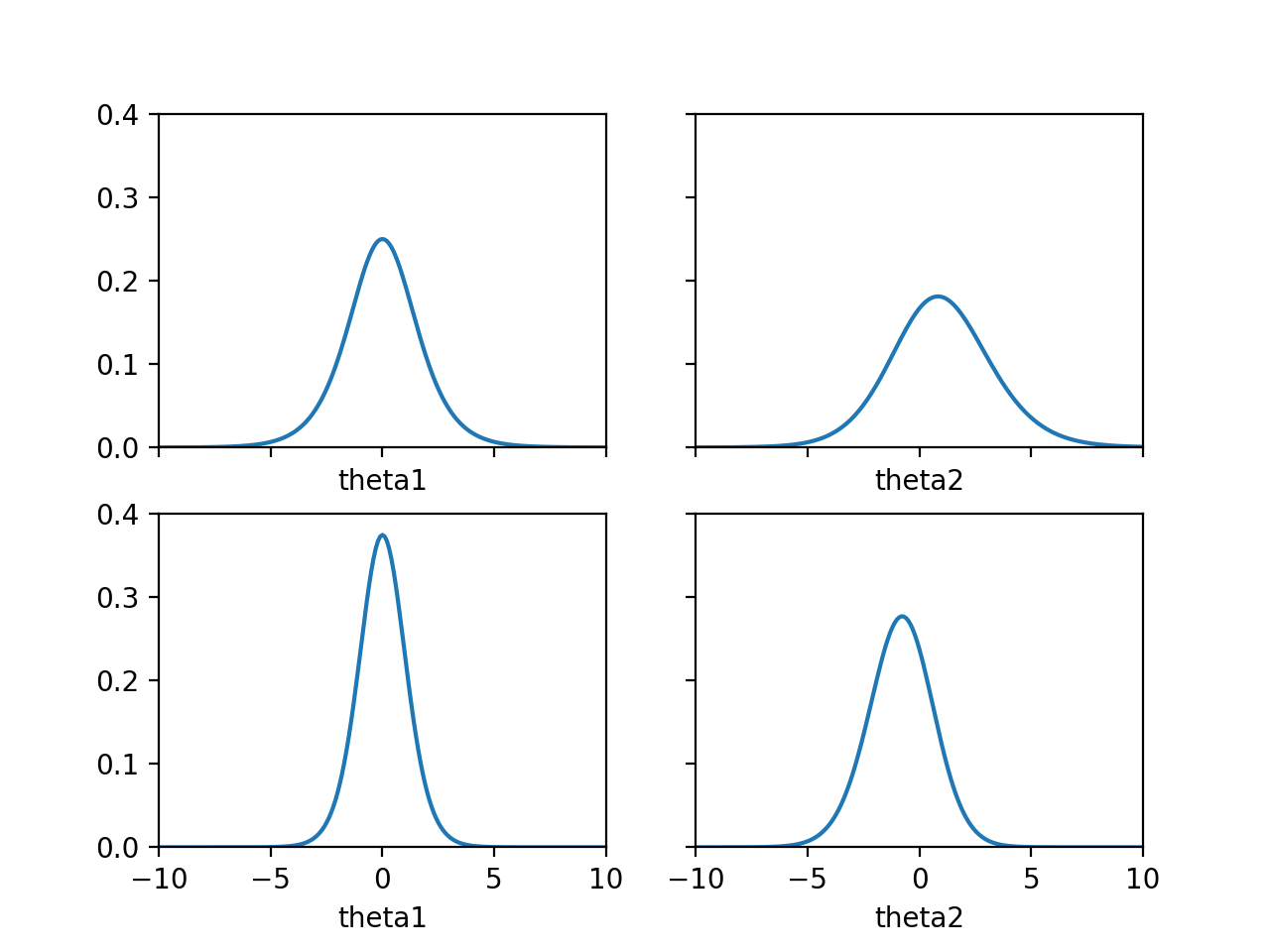
\(\theta_1\)은 \(0\)일 확률이 높고, \(\theta_2\)는 \(-0.7\)일 확률이 높은 것을 알 수 있습니다.

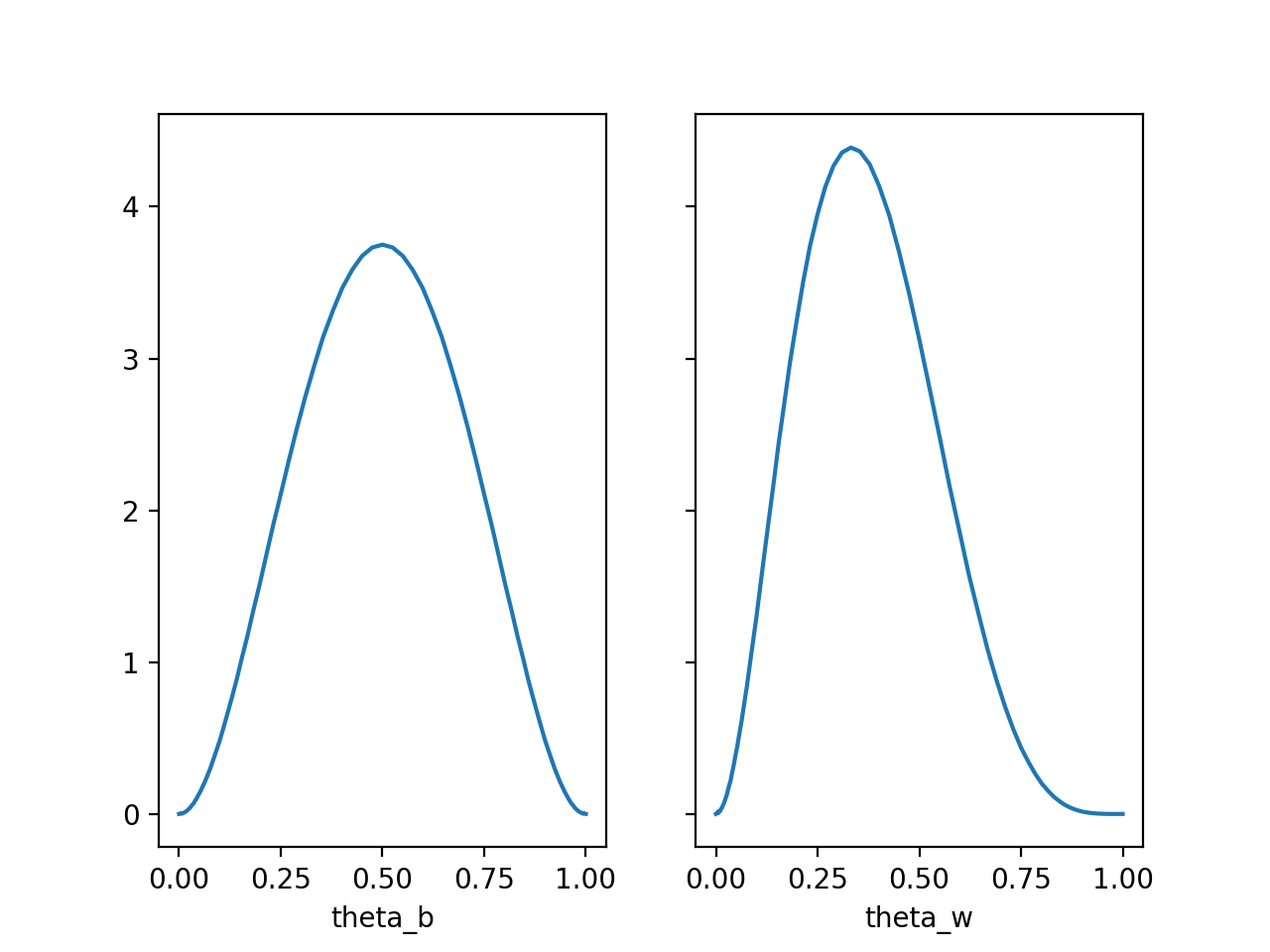
\(\theta_1\)과 \(\theta_2\)을 이용해서 \(\theta_b\)와 \(\theta_w\)을 그려서 살펴보면 다음과 같은 결론을 내릴 수 있습니다.

• 검은색 동전을 던져서 앞면이 나올 확률인 \(\theta_b\)는 \(0.5\)일 확률이 높습니다.
• 흰색 동전을 던져서 앞면이 나올 확률인 \(\theta_w\)는 \(0.33\)일 확률이 높습니다.

직관적으로 생각해 보면, Data를 살펴보았을 때 검은색 동전의 경우에 네 번 동전을 던졌을 때 두 번 앞면이 나왔으며, 흰색 동전의 경우에는 여섯 번 동전을 던졌을 때 두 번 앞면이 나와서, 각각의 앞면이 나올 확률은 \(\frac{1}{2}\)과 \(\frac{1}{3}\)일 것으로 추측되는데, 이것은 계산결과와 일치합니다.

계산과정을 살펴보면서 느낄 수 있었겠지만, Likelihood를 어떻게 정하느냐에 따라 결론이 바뀔 수가 있습니다. 여기서 정한 Likelihood도 이 문제를 풀면서 정한 임의의 방법중 하나일 뿐, 이렇게 정해야 된다는 법은 없습니다. 적절한 결론을 이끌어내기 위해서는 적절하게 Likelihood를 정의하는게 중요합니다. MNIST 필기체 숫자 인식을 위한 Machine Learning Model을 설계할 때도 Fully Connected Layer로 설계할 수도 있지만 Convolutional Neural Network로 설계하게 되면 Parameter 수도 훨씩 적게 쓰면서 훨씬 높은 정확도의 Model을 설계할 수 있습니다. 여기에서도 \(\theta_1\)과 \(\theta_2\)를 Parameter로 사용했는데 같은 문제를 풀더라도 푸는 방법에 따라 Parameter의 수가 매우 적거나 매우 많아질 수 있으며 Parameter 수가 동일하더라도 Likelihood의 구조에 따라 결과가 매우 달라질 수 있습니다.

여기서는 단순히 검은색 동전, 흰색 동전을 예로 들어서 설명했지만 구멍이 있는 네모난 빨간색 동전 처럼 다양한 Feature가 추가될 수 있습니다. 이런 경우에는 어떤 것을 어떤 형태로 Feature로 정의하고, Feature들 간에 어떤 관계가 있을지 정의하고, 어떤 것을 찾아야 되는 Parameter로 할지 등을 정의해야 하며, 이것은 단순히 동전 던지기가 아니라 아주 다양하게 여러가지 형태로 응용될 수 있습니다.

Coin Toss - Markov Chain Monte Carlo

Coin Toss - Additional Feature를 보면 Parameter가 \(\theta_1\)과 \(\theta_2\)가 있는데 이 Parameter로 조합할 수 있는 모든 경우에 대해 는 Posterior를 계산할 때 Data를 한 개씩 넣어서 계산했습니다. 이런 계산방식은 Parameter의 수가 적을 때는 계산이 가능하지만 Parameter의 수가 많아지면 현실적으로 계산이 불가능합니다. 그래서 Parameter의 수가 많아지면 좀 더 효율적인 계산방법이 필요한데 이때 많이 사용되는 방법이 Markov Chain Monte Carlo Method입니다.

여기서는 Coin Toss - Additional Feature에서 푼 문제와 동일한 문제를 Markov Chain Monte Carlo Method중에 하나인 Metropolis Hastings Algorithm을 사용해서 풀어보도록 하겠습니다.

풀어야 되는 수식을 다시 적어보면 다음과 같습니다.

\[p(\theta_1, \theta_2 \mid D_1=1, D_2=1)=\frac{p(D_1=1, D_2=1 \mid \theta_1, \theta_2)p(\theta_1, \theta_2)}{p(D_1=1, D_2=1)}\]

\(D_1\)과 \(D_2\)가 주어졌을 때 \(\theta_1\)과 \(\theta_2\)가 어떤 값을 가지고 있을 확률이 높은지를 계산해야 합니다.

Metropolis Hastings Algorithm은 다음과 같습니다.

1. \(t\)를 \(1\)로 정의합니다.
2. 적당히 아무 값을 골라서 \(\theta_{1,t}\)와 \(\theta_{2,t}\)라고 정의합니다.
3. \(p(\theta_{1,t}, \theta_{2,t} \mid D_1=1, D_2=1)\)를 계산하고 이 값을 \(p_t\)라고 정의합니다.
4. \(\theta_{1,t}\)와 \(\theta_{2,t}\)에서 조금 다른 적당한 아무 값을 골라서 \(\theta_{1,t+1}\)와 \(\theta_{2,t+1}\)라고 정의합니다.
5. \(p(\theta_{1,t+1}, \theta_{2,t+1} \mid D_1=1, D_2=1)\)를 계산하고 이 값을 \(p_{t+1}\)라고 정의합니다.
6. \(\frac{p_{t+1}}{p_t}\ge1\)이면 \(t:=t+1\)을 실행하고 4부터 다시 실행합니다.
7. \(\frac{p_{t+1}}{p_t}<1\)이면 \(\frac{p_{t+1}}{p_t}\)의 확률로 \(t:=t+1\)을 실행하고 4부터 다시 실행합니다.
8. (\(\theta_{1,t+1}\), \(\theta_{2,t+1}\), \(p_{t+1}\)을 버리고) 4부터 다시 실행합니다.

이 과정을 충분히 여러번 반복해서 충분한 수의 \(\theta_1\)과 \(\theta_2\)를 확보하고 여기서 모인 값들을 모아서 분포를 살펴보면 (여기서 증명은 하지 않겠습니다만) \(p(\theta_1, \theta_2 \mid D_1=1, D_2=1)\)의 Distribution과 유사합니다.

이렇게 Sample을 하면 초반에 뽑힌 Sample들은 Distribution에 속해 있다고 보기 힘든(\(p(\theta_1, \theta_2 \mid D_1=1, D_2=1)\)의 값이 작은) Sample들이 많이 포함되게 됩니다. 그래서 초반 Sample들은 사용하지 않고 버리는 것이 일반적인데, 이렇게 버리는 Sample의 기간을 Burn-In Period라고 부릅니다.

4에 보면 조금 다른 적당한 아무 값을 고른다고 되어 있는데 보통은 Normal Distribution에서 작은 값을 Sample하고 Sample된 값을 더해서 고르는 것이 일반적입니다. 이때 Normal Distribution에 너무 크거나 너무 작지 않은 적당한 Standard Deviation를 설정합니다.

이 계산을 할 때 중간에 \(\frac{p_{t+1}}{p_t}\)를 계산해야 되는데 계산해 보면 다음과 같이 정리되기 때문에 Evidence는 계산하지 않아도 되고 Likelihood와 Prior만 계산하면 됩니다.

\[\begin{aligned} \frac{p_{t+1}}{p_t} &=\frac{p(\theta_{1,t+1}, \theta_{2,t+1} \mid D_1=1, D_2=1)}{p(\theta_{1,t}, \theta_{2,t} \mid D_1=1, D_2=1)} \\ &= \frac{\frac{p(D_1=1, D_2=1 \mid \theta_{1,t+1}, \theta_{2,t+1})p(\theta_{1,t+1}, \theta_{2,t+1})}{p(D_1=1, D_2=1)}}{\frac{p(D_1=1, D_2=1 \mid \theta_{1,t}, \theta_{2,t})p(\theta_{1,t}, \theta_{2,t})}{p(D_1=1, D_2=1)}} \\ &=\frac{p(D_1=1, D_2=1 \mid \theta_{1,t+1}, \theta_{2,t+1})p(\theta_{1,t+1}, \theta_{2,t+1})}{p(D_1=1, D_2=1 \mid \theta_{1,t}, \theta_{2,t})p(\theta_{1,t}, \theta_{2,t})} \end{aligned}\]

import math
from collections import defaultdict
import matplotlib.pyplot as plt
import numpy as np

min_p = 0
max_p = 0.4
min_theta = -10
max_theta = 10
num_digits = 1
num_steps = 200

mcmc_init_theta = 0.0
mcmc_jump_sigma = 1.0
mcmc_burn_in = 1000
mcmc_num_samples = 100000

def new_uniform_pdf():
  pdf = defaultdict(float)
  for i in range(num_steps):
    for j in range(num_steps):
      pdf[
          round(
              min_theta + i / num_steps * (max_theta - min_theta), num_digits),
          round(
              min_theta + j / num_steps * (max_theta - min_theta), num_digits)
      ] = 1 / (max_theta - min_theta) ** 2
  return pdf

def prior(pdf, theta1, theta2):
  return pdf[round(theta1, num_digits), round(theta2, num_digits)]

def sigmoid(x):
  return 1 / (1 + math.exp(-x))

def likelihood(x1, x2, theta1, theta2):
  p = 1
  for i1, i2 in zip(x1, x2):
    t = sigmoid(theta1 + theta2 * i2)
    if i1 == 0:
      p *= (1 - t)
    else:
      p *= t
  return p

def normalize(pdf, dim):
  s = sum(pdf.values()) * (((max_theta - min_theta) / num_steps) ** dim)
  for k in pdf:
    pdf[k] /= s

def jump(theta):
  new_theta = None
  while new_theta is None or new_theta < min_theta or new_theta > max_theta:
    new_theta = np.random.normal(theta, mcmc_jump_sigma)
  return round(new_theta, num_digits)

def is_reject(p1, p2):
  if 0.0 <= p2 - p1:
    return False
  if np.random.rand() < p2 / p1:
    return False
  return True

def posterior(prior_pdf, x1, x2, init_theta1, init_theta2):
  posterior_pdf = defaultdict(float)
  theta1_posterior_pdf = defaultdict(float)
  theta2_posterior_pdf = defaultdict(float)

  theta1 = init_theta1
  theta2 = init_theta2

  for _ in range(mcmc_burn_in):
    p1 = likelihood(x1, x2, theta1, theta2) * prior(prior_pdf, theta1, theta2)
    new_theta1 = jump(theta1)
    new_theta2 = jump(theta2)
    p2 = likelihood(x1, x2, new_theta1, new_theta2) * prior(prior_pdf,
        new_theta1, new_theta2)
    if not is_reject(p1, p2):
      theta1 = new_theta1
      theta2 = new_theta2

  for _ in range(mcmc_num_samples):
    p1 = likelihood(x1, x2, theta1, theta2) * prior(prior_pdf, theta1, theta2)
    new_theta1 = jump(theta1)
    new_theta2 = jump(theta2)
    p2 = likelihood(x1, x2, new_theta1, new_theta2) * prior(prior_pdf,
        new_theta1, new_theta2)
    if not is_reject(p1, p2):
      theta1 = new_theta1
      theta2 = new_theta2
      posterior_pdf[(theta1, theta2)] += 1
      theta1_posterior_pdf[theta1] += 1
      theta2_posterior_pdf[theta2] += 1

  normalize(posterior_pdf, 2)
  normalize(theta1_posterior_pdf, 1)
  normalize(theta2_posterior_pdf, 1)

  return \
      posterior_pdf, theta1_posterior_pdf, theta2_posterior_pdf, theta1, theta2

def ax_plot(ax, fig, pdf, label):
  pdf = dict(sorted(pdf.items()))
  ax.plot(pdf.keys(), pdf.values())
  ax.set_xlim([min_theta, max_theta])
  ax.set_ylim([min_p, max_p])
  ax.set_xlabel(label)

def ax_tricontour(ax, fig, pdf, label, label2):
  tricontour = ax.tricontour(*zip(*pdf), list(pdf.values()), levels=100,
      vmin=0.0, vmax=0.15, cmap='jet')
  ax.set_xlim([min_theta, max_theta])
  ax.set_ylim([min_theta, max_theta])
  ax.set_xlabel(label)
  ax.set_ylabel(label2)
  fig.colorbar(tricontour, ax=ax)

data = [[1, 0, 1, 1, 0], [0, 0, 0, 1, 0]]
data2 = [[1, 0, 0, 1, 1], [1, 1, 0, 0, 1]]
fig1, axs1 = plt.subplots(len(data), sharex=True, sharey=True)
fig2, axs2 = plt.subplots(len(data), 2, sharex=True, sharey=True)
pdf = new_uniform_pdf()
theta1 = mcmc_init_theta
theta2 = mcmc_init_theta
for i, (x1, x2) in enumerate(zip(data, data2)):
  pdf, theta1_pdf, theta2_pdf, theta1, theta2 = posterior(
      pdf, x1, x2, theta1, theta2)
  tricontour = ax_tricontour(axs1[i], fig1, pdf, 'theta1', 'theta2')
  ax_plot(axs2[i, 0], fig2, theta1_pdf, 'theta1')
  ax_plot(axs2[i, 1], fig2, theta2_pdf, 'theta2')
fig1.savefig('bayes04_1.png', dpi=200)
fig2.savefig('bayes04_2.png', dpi=200)

fig3, axs3 = plt.subplots(1, 2, sharex=True, sharey=True)
theta_b = defaultdict(float)
theta_w = defaultdict(float)
for i in range(num_steps):
  for j in range(num_steps):
    theta1 = round(
        min_theta + i / num_steps * (max_theta - min_theta), num_digits)
    theta2 = round(
        min_theta + j / num_steps * (max_theta - min_theta), num_digits)
    theta_b[round(sigmoid(theta1), 3)] += prior(pdf, theta1, theta2)
    theta_w[round(sigmoid(theta1 + theta2), 3)] += prior(pdf, theta1, theta2)
theta_b = dict(sorted(theta_b.items()))
axs3[0].plot(theta_b.keys(), theta_b.values())
axs3[0].set_xlabel('theta_b')
theta_w = dict(sorted(theta_w.items()))
axs3[1].plot(theta_w.keys(), theta_w.values())
axs3[1].set_xlabel('theta_w')
fig3.savefig('bayes04_3.png', dpi=200)

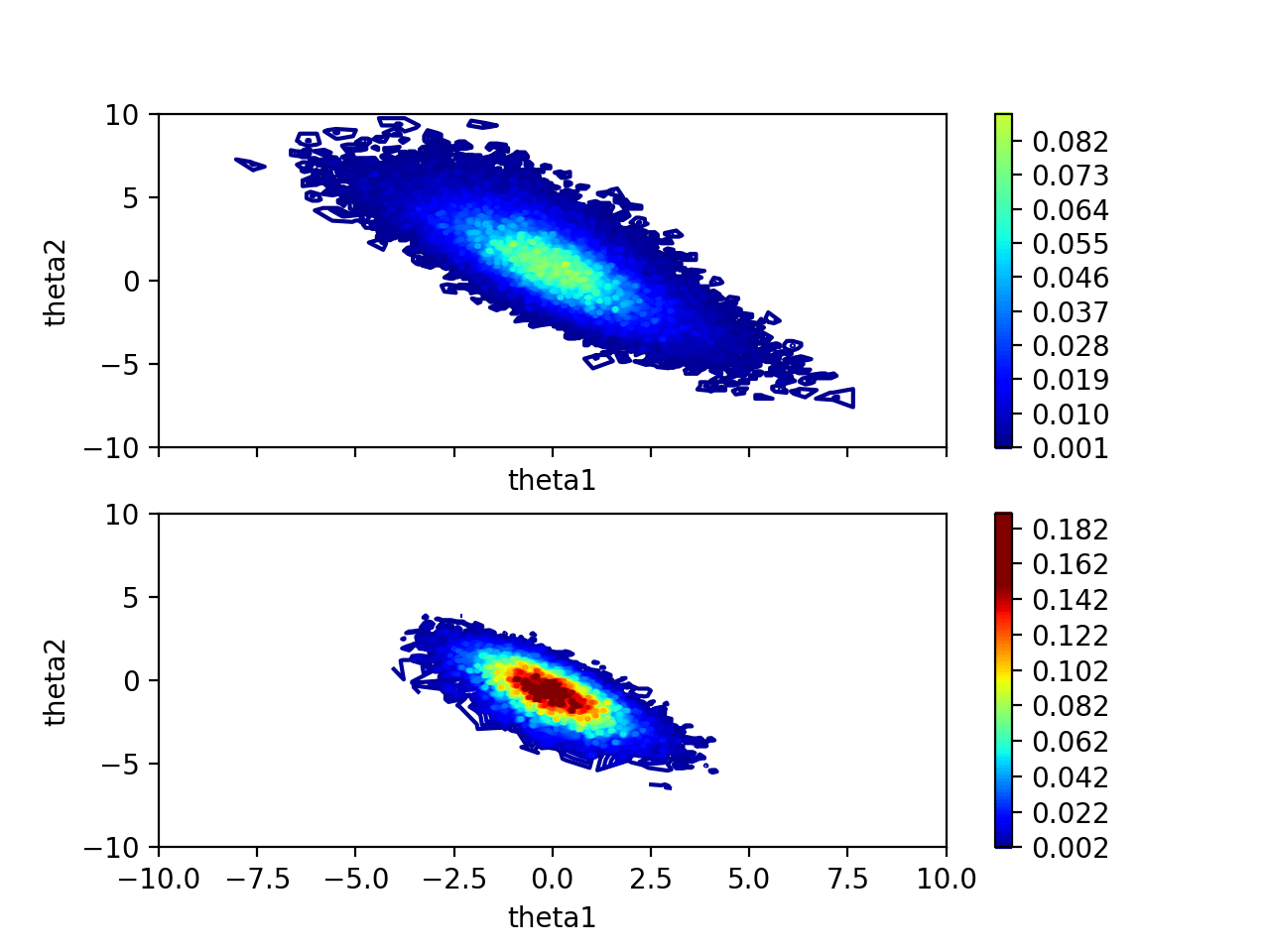
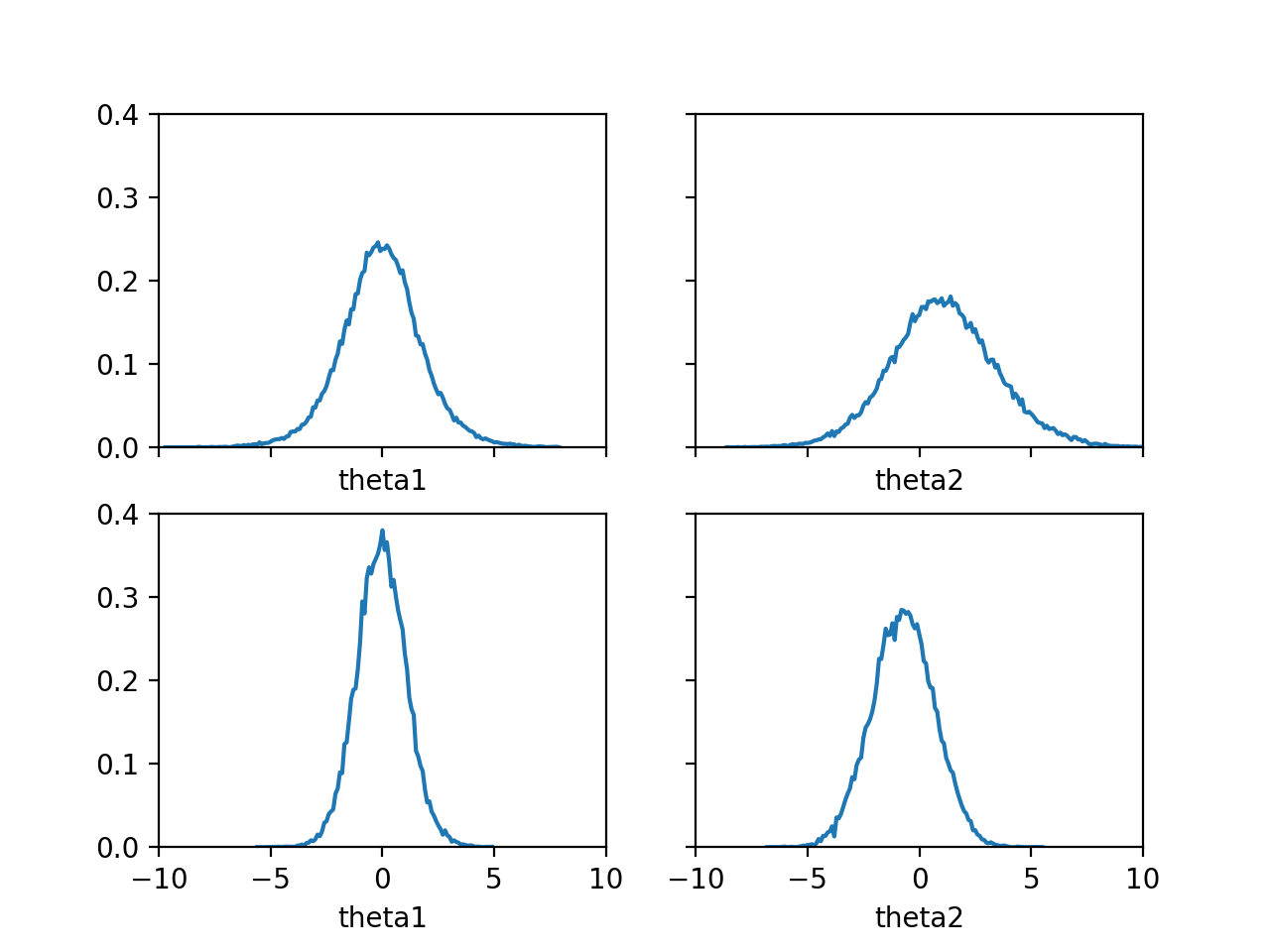
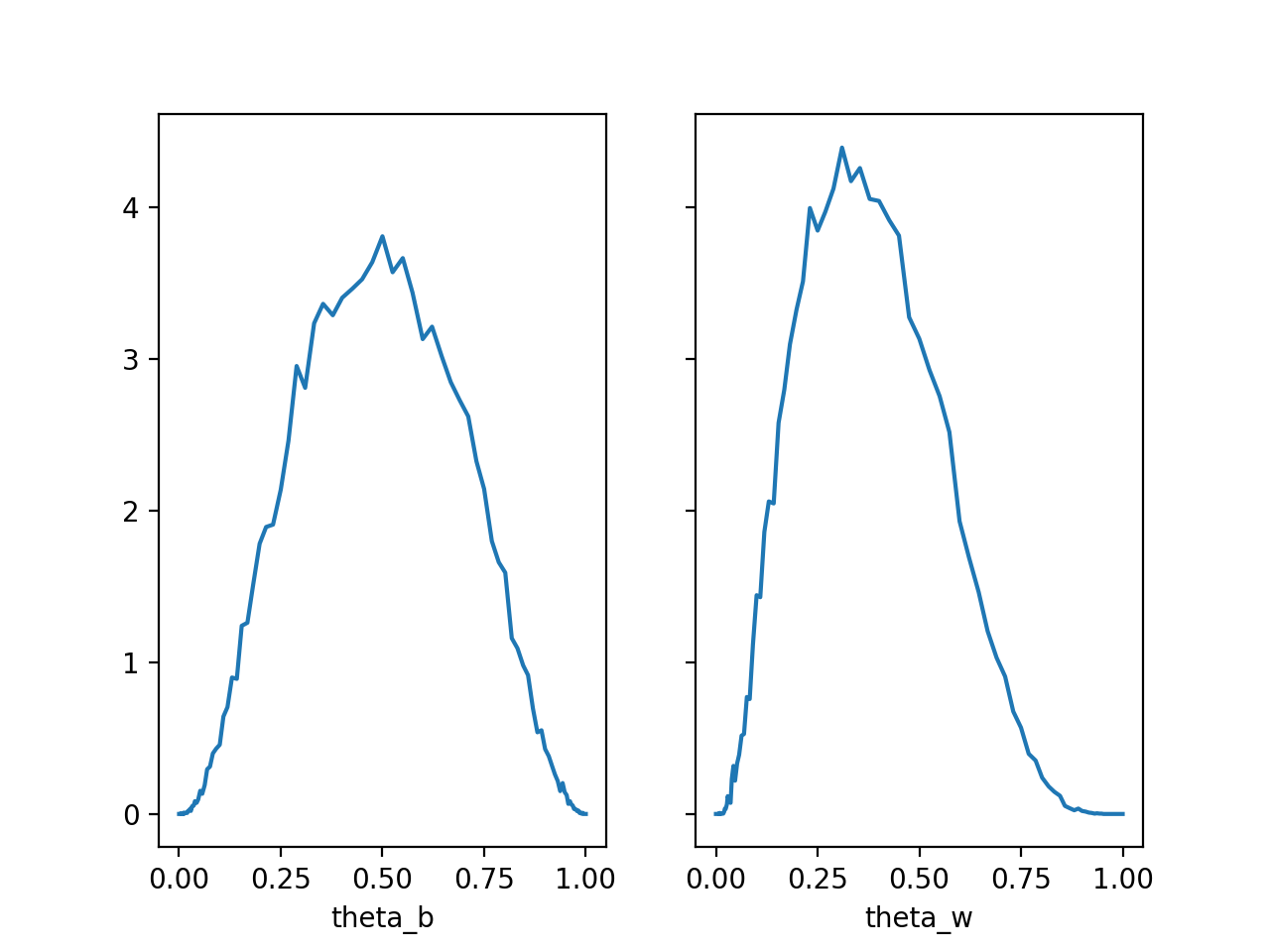
결과를 확인해 보면 Coin Toss - Additional Feature의 결과와 유사합니다. Coin Toss - Markov Chain Monte Carlo 오히려 결과가 더 안 좋아 보일 수도 있지만, 이 방법은 Parameter의 수가 많아졌을 때도 범용적으로 사용할 수 있는 장점이 있습니다.

그리고 여기서는 Markov Chain Monte Carlo Method중에 Metropolis Hastings Algorithm을 사용해서 계산했지만 Markov Chain Monte Carlo Method에는 Metropolis Hastings Algorithm이외에도 많은 다양한 더 좋은 방법이 존재합니다.

Coin Toss - PyMC

Coin Toss - Markov Chain Monte Carlo에서는 번거롭게 Markov Chain Monte Carlo Method를 직접 구현해서 계산했습니다. 하지만 이것은 PyMC를 이용하면 매우 쉽게 계산할 수 있습니다.

여기서는 Coin Toss - Markov Chain Monte Carlo에서 푼 문제와 동일한 문제를 PyMC를 사용해서 풀어보도록 하겠습니다.

import math
from collections import defaultdict
import numpy as np
import matplotlib.pyplot as plt
import arviz as az
import pymc as pm

min_theta = -10
max_theta = 10

data = np.array([1, 0, 1, 1, 0, 0, 0, 0, 1, 0])
data2 = np.array([1, 0, 0, 1, 1, 1, 1, 0, 0, 1])

model = pm.Model()
with model:
  theta1 = pm.Uniform('theta1', lower=min_theta, upper=max_theta)
  theta2 = pm.Uniform('theta2', lower=min_theta, upper=max_theta)
  logit = theta1 + theta2 * data2
  obs = pm.Bernoulli('obs', logit_p=logit, observed=data)
  pm.Deterministic('theta_b', pm.math.sigmoid(theta1))
  pm.Deterministic('theta_w', pm.math.sigmoid(theta1 + theta2))
  idata = pm.sample(10000)

stacked = az.extract(idata)
theta1_sample = stacked.theta1.values
theta2_sample = stacked.theta2.values

ax = az.plot_kde(theta1_sample, theta2_sample,
    contour_kwargs={'colors': None, 'cmap': 'jet', 'levels': 100})
ax.set_xlabel('theta1')
ax.set_ylabel('theta2')
fig = ax.figure
fig.savefig('bayes05_1.png')

axes = az.plot_trace(idata, combined=True)
fig = axes.ravel()[0].figure
fig.tight_layout()
fig.savefig('bayes05_2.png')

Coin Toss - Markov Chain Monte Carlo보다 Code가 많이 간결해졌습니다.

\(\theta_1\)과 \(\theta_2\)는 최소값은 \(-10\)이고 최대값은 \(10\)인 Uniform Distribution으로 Prior를 설정합니다. Likelihood는 \(sigmoid(\theta_1+\theta_2 D_2)\)를 \(p\)로 가지는 Bernoulli Distribution을 따르도록 설정합니다. Bernoulli Distribution의 logit_p에 설정하면 \(sigmoid\)가 자동으로 적용됩니다. \(\theta_b\)와 \(\theta_w\)값을 살펴보기 위해 Deterministic을 사용해서 \(sigmoid(\theta_1)\)과 \(sigmoid(\theta_1+\theta_2)\)로 정의합니다. 10000개의 Sample을 뽑도록 설정했으며, tune(burn in)은 설정하지 않으면 Default로 1000으로 설정됩니다.

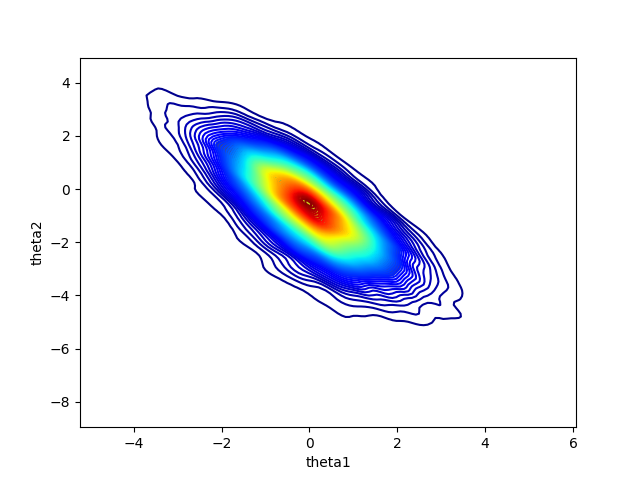
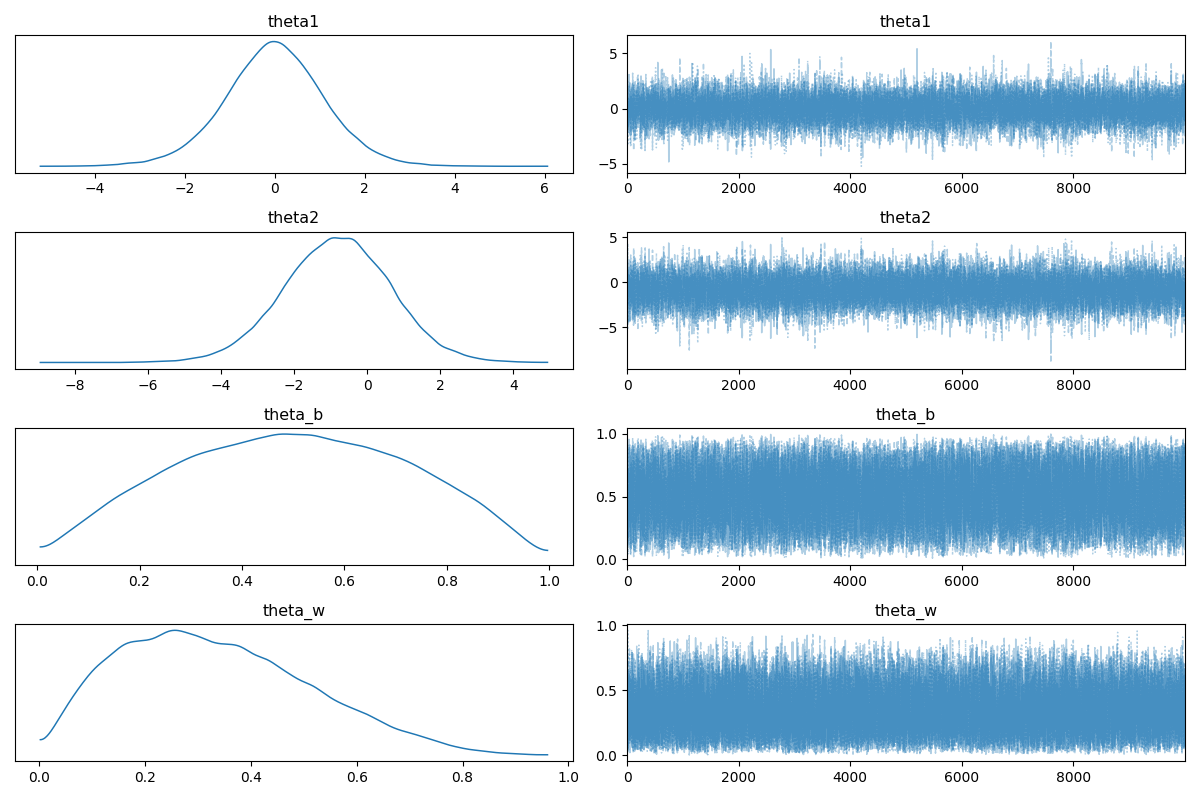
결과를 확인해 보면 Coin Toss - Markov Chain Monte Carlo의 결과와 유사합니다.

Conclusion

이 글에서는 Bayes Theorem의 기본적인 내용을 살펴 보았습니다. 이해를 최대한 돕기 위해 너무 추상적으로 설명하는 것을 피하면서 최대한 이해하기 쉬운 문제를 가지고 구체적인 계산을 통해 설명하기 위해 노력하였습니다. Bayes Theorem의 이해에 어려움이 있는 많은 분들에게 조금이라도 도움이 되었으면 좋겠습니다.